Application qui conserve la convergence

[Nightmare]

Salut à tous :happy3:

Je ne sais pas si le problème a déjà été posé, mais je suis retombé dessus en ouvrant mon Leichtnam ce matin, je le trouve vraiment magnifique et me permet de le poster :

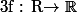
Soit telle que pour toute série convergente , la série est également convergente.

Décrire le comportement de f au voisinage de 0.

Amusez-vous bien :happy3:

[yos]

f(x)=O(x) ???

[Nightmare]

Salut yos :happy3:

Oui ceci est vrai mais on peut trouver encore plus précis ! En fait on peut même décrire localement f et non seulement son comportement.

[Ben314]

Je pense que le mot "convergente" est évidement à prendre au sens des "limites des sommes partielles" et pas au sens "somabilité".
La réponse f(x)=O(x) serait la bonne au sens "somabilité" (si je ne m'abuse) mais elle n'est pas sufisante pour la suite (-1)^n/n...

J'ai bon ?

[Nightmare]

Oui on parle de convergence des sommes partielles. Cela dit la question est intéressant si on parle seulement de sommabilité, je ne crois pas que f(x)=O(x) soit suffisant dans ce cas. Je vais regarder ça après manger.

:happy3:

[Ben314]

Juste pour faire le "tatillon",
Il me semble que, dans le cas de la somabilité, f(x)=O(x) est clairement suffisant ce qui est moins clair c'est que c'est nécessaire

[Nightmare]

Oui je voulais bien sûr dire nécessaire merci de la correction.

[Ben314]

Je pense avoir aussi la nécessité...
(mais je suis en train de "noyer le poisson" puisque je ne répond pas à la question de départ...)
(En plus, j'ai un boulot monstre cet aprés midi, il FAUT que je décroche de ce P... d'ordinateur)

[Ben314]

Pour la question de départ, j'ai l'impression (???) que, SI f ADMET UN D.L. A L'ORDRE k en 0 alors ce D.L est de la forme :
f(x)=ax+rien_du_tout+o(x^k)
(Pour cela, j'exhibe des suites u_n telles que le série de u_n soit convergente mais pas la série des (u_n)^k)

J'intuite donc une solution de la forme
f(x)-ax=o(tout_ce_qu'on_veut_ou_presque)
mais je n'ose pas croire à
f(x)=ax sur [-epsilon,epsilon]

[yos]

Quelle série échappe à ?

[Ben314]

SI JE NE M'ABUSE, la série dont la n-ième somme partielle est égale à avec
(mais ca serait bien que tu vérifie...)

[Doraki]

f(x) est dérivable en 0.
f est impaire au voisinage de 0 ?

Non ben en fait je crois bien que f doit être carrément linéaire au voisinage de 0.

Pour yos : (u_3n, u_3n+1, u_3n+2) = (n^(-1/3), -n^(-1/3)/2, -n^(-1/3)/2).

[yos]

la série dont la n-ième somme partielle est égale à avec

J'ai du mal à voir car c'est u_n qu'on met au cube.

Pour yos : (u_3n, u_3n+1, u_3n+2) = (n^(-1/3), -n^(-1/3)/2, -n^(-1/3)/2).

OK. Je me doutais qu'on pouvait fabriquer un machin comme ça.

[Ben314]

Si alors puis et, quand tu somme, il te reste des constantes, du qui tend vers 0 et une somme de ET C'EST LA QUE JE ME SUIS GOURRE.

La soluce de doraki marche !!!

Rajout : je viens juste de réagir que, dans C, les suite avec une racine p-ième de l'unité donnent des exemples trés simple et font "entrevoir" la soluce de doraki.

[Nightmare]

Salut à tous :happy3:

Doraki > L'intuition est bonne, f est bien une homothétie autour de 0. Je te laisse chercher comment montrer ça. Tu es bien parti en disant que f est impaire au voisinage de 0.

[Doraki]

On suppose f pas impaire au voisinage de 0.
Alors il existe une suite xn qui tend vers 0 telle que f(xn) <> -f(-xn).
Quitte à en prendre une sous-suite, on peut considérer que f(xn) + f(-xn) est toujours positif.

On prend alors une suite yn qui est l'aplatissement de la suite de séquences finies :
Pour n entier, On prend un entier k > 1/(f(xn)+f(-xn)), et on définit
(yn)(2m) = xn pour 1 <= m <= k,
(yn)(2m+1) = -xn pour 1 <= m <= k.

La suite aplatie yn ainsi obtenue donne une série qui converge vers 0.
En revanche, la série de terme f(xn) diverge vers l'infini.

On a donc une contradiction.
Ainsi, f est impaire.

On embraye sur la partie 2 :

On suppose qu'il existe une suite (xn) positive qui tend vers 0 telle que f(xn)/xn <> f(xn+1)/xn+1.

On redéfinit une suite aplatie en combinant à l'étape i des xi avec des -x(i+1) et peut avoir une contradiction.

[Nightmare]

Ok pour la 1), pour la 2) je ne vois pas la contradiction à moins que j'ai mal compris la construction de ta suite.

[ffpower]

je n ai pas tres bien compris le point 2 de doraki moi non plus. Pour ma part,j avais deja réfléchi a cet exo dans le passé: J avais commencé par montrer l imparité par la meme methode que doraki, puis j ai conclus par l argument suivant:(J ai montré que f était additive au voisinage de 0 par la meme methode que pour l imparité,sauf qu au lieu de juxtaposer des xn,-xn,j ai juxtaposé des xn,yn,-xn-yn)

[Nightmare]

je n ai pas tres bien compris le point 2 de doraki moi non plus. Pour ma part,j avais deja réfléchi a cet exo dans le passé: J avais commencé par montrer l imparité par la meme methode que doraki, puis j ai conclus par l argument suivant:(J ai montré que f était additive au voisinage de 0 par la meme methode que pour l imparité,sauf qu au lieu de juxtaposer des xn,-xn,j ai juxtaposé des xn,yn,-xn-yn)

Salut ffpower :happy3:

Certes, et il reste à montrer que f est continue pour conclure toujours par le même type d'argument.

:happy3:

[Doraki]

J'ai pas eu le temps de finir correctement hier soir, je le refais :

On suppose qu'il existe deux suites (xn) positive et (yn) négative qui tendent vers 0, telles que f(xn)/xn <> f(yn)/yn ; |xn| < 1/n², |yn| < 1/n².

A l'étape n, on prend 2 entiers positifs k et k' tels que
|k*xn + k'*yn| < 1/n², et
|k*f(xn) + k'*f(yn)| > n.
C'est possible en prenant approximativement k' = - xn*k/yn, et
k > n/(xn * |f(xn)/xn-*f(yn)/yn|).
Pour faire notre séquence à cette étape n, on mélange alors k termes xn et k' termes yn dans notre suite de sorte que la somme partielle ne dépasse jamais |xn| ni |yn| en valeur absolue.

En mettant bout à bout toutes ces séquences, on obtient une suite (zn) telle que la somme des zn converge, et la somme des f(zn) diverge complètement.
On a une contradiction, et on peut en conclure que f est linéaire au voisinage de 0.