Application qui conserve les vecteurs unitaires
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Mai 2009, 14:07
par Nightmare » 09 Mai 2009, 14:07
Bonjour à tous :happy3:
Voici un problème que je me suis posé et dont je n'ai toujours pas trouvé de solution :marteau:
On considère une application f (a priori pas forcément affine) du plan dans lui même et telle qu'elle envoie tout couple de point de distance 1 sur un couple de point de distance 1.
Autrement dit,
=1\Rightarrow d(f(A),f(B))=1)
.
J'ai conjecturé que f était une isométrie, seulement je n'arrive pas à le prouver... Je ne sais pas s'il faut que f soit affine, je ne trouve pas de contre-exemple !
Si vous avez des idées à partager !
Merci :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Mai 2009, 14:10
par Nightmare » 09 Mai 2009, 14:10
Il me semble que le problème peut s'élargir dans un hyperespace
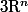
quelconque.
Edit : Sauf pour n=1
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Mai 2009, 19:36
par Nightmare » 10 Mai 2009, 19:36
Pas d'idées?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Mai 2009, 20:41
par yos » 10 Mai 2009, 20:41
Salut.
Si f est affine, c'est clair.
Il faut donc pas la supposer affine.
Tu veux dire que ça marche pas pour n=1 ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Mai 2009, 20:57
par Nightmare » 10 Mai 2009, 20:57
Oui, c'est bien le cas non?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Mai 2009, 21:59
par yos » 10 Mai 2009, 21:59
En effet, je crois que f(x)=x+1 ou x selon que x est entier ou pas est un contre-exemple.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Mai 2009, 22:40
par Nightmare » 10 Mai 2009, 22:40
Je pense avoir trouvé quelque chose. Imod aimerait surement ce problème !
On sait uniquement que f conserve la distance 1. On peut essayer de voir si f conserve quelques figures. Il s'avère que f envoie les triangles équilatéraux sur des triangles équilatéraux.
En composant avec une certaine isométrie on obtient une fonction h qui conserve la distance 1 et qui envoie les triangles équilatéraux sur des triangles équilatéraux.
Ce qu'on peut alors faire, c'est paver le plan par des triangles équilatéraux de côté 1.
C'est là où je bloque. En fait j'aurais envie de montrer que h va fixer tous les autres triangles équilatéraux et finalement fixer le plan entier ce qui prouvera que f est une isométrie.
Mais là je n'arrive pas à prouver justement que h va fixer tous les autres triangles équilatéraux.
Une idée pour débloquer?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Mai 2009, 22:45
par Nightmare » 10 Mai 2009, 22:45
Bon en fait c'est évident que si on fixe les sommets d'un triangle équilatéral de côté 1 on fixe tous les sommets des triangles du pavage.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 16:22
par Nightmare » 11 Mai 2009, 16:22
Pas d'idée?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Mai 2009, 17:15
par Doraki » 11 Mai 2009, 17:15
Tu devrais préciser tes hypothèses.
La fonction doit-elle être continue ? injective ?
Une fonction qui n'est ni l'un ni l'autre peut par exemple envoyer tous les sommets du pavage sur un seul triangle équilatéral.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 18:03
par Nightmare » 11 Mai 2009, 18:03
Salut Doraki !
Je vois mal comment on pourrait envoyer tous les sommets sur un seul triangle équilatéral si l'on doit conserver la distance 1.
Prenons déjà le pavage en triangle équilatéral de côté 1 d'un hexagone régulier de côté 1. On suppose qu'un des triangles est fixé. Il reste 4 sommets à envoyer sur A, B et C, forcément, une des arête va être envoyée sur un point !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 18:26
par Nightmare » 11 Mai 2009, 18:26
Au temps pour moi ce que je viens de dire est faux !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 18:27
par Nightmare » 11 Mai 2009, 18:27
Cela dit je ne crois quand même pas qu'on puisse envoyer tous les sommets sur un seul triangle équilatéral !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 18:33
par Nightmare » 11 Mai 2009, 18:33
J'en suis certain même, un losange de côté 1 est envoyé sur un losange de côté 1 et non un triangle équilatéral.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Mai 2009, 19:19
par Doraki » 11 Mai 2009, 19:19
Regarder la fonction seulement sur les sommets du pavages ne permet pas de donner une contradiction.
Il suffit de choisir f(n+m*j) en fonction de n+m modulo 3.
En revanche si on regarde un graphe formé par 4 triangles équilatéraux ABC ADE BCF DEG avec d(F,G) = 1, on voit que d(f(A),f(F)) ainsi que d(f(A),f(G)) ne peut être que 0 ou sqrt(3).
Ainsi, si f(A) = f(F) il est impossible de trouver un f(G) qui satisfasse toutes les contraintes.
Donc finalement, l'image d'un losange comme ABFC doit rester un losange, et on peut en déduire que l'image du pavage doit rester un pavage.
Reste à voir ce qu'on peut faire avec tous les autres points.
 par busard_des_roseaux » 11 Mai 2009, 20:35
par busard_des_roseaux » 11 Mai 2009, 20:35
bonsoir,
comme il existe un triangle équilatéral de coté

, de rayon
de cercle circonscrit 1. Que le symétrique de son centre O , par rapport aux milieu des côtés, appartient aussi
au cercle circonscrit, on peut montrer que
=\sqrt{3})
implique
,f(B))=d(A,B))
puis
=\sqrt{3}^n)
implique
,f(B))=d(A,B))
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 22:34
par Nightmare » 11 Mai 2009, 22:34
Salut à vous deux :happy3:
Ok, les sommets sont invariants par h. Si on prouve qu'il en va de même pour les côtés alors c'est gagné, tout le plan sera invariant.
Busard des roseaux > Bien joué. Ca peut peut être être utile de savoir que la distance

est fixée par f (et h), notamment pour un argument de densité :

est dense dans
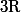
.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Mai 2009, 23:22
par ffpower » 11 Mai 2009, 23:22
Bonsoir!
Si par hasard on montre si on montre que toute distance appartenant a D=(Z+\sqrt(3)Z)inter R+* est fixee par f,alors c est gagné.En effet,si d/2 appartient a V,si on a 2 points x et y de distance inferieure a d,alors il existe un point z a distance d/2 de x et y.f(z) est alors a distance d/2 de f(x) et f(y) donc la distance entre f(x) et f(y) est inferieure a d.d pouvant etre absolument petit,on en deduit la continuité de f.De plus,on obtient que f est affine sur des pavages du plan arbitrairement fin,donc on peut conclure par continuité.Reste plus qu a..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 23:26
par Nightmare » 11 Mai 2009, 23:26
Salut ffpower :happy3:
"On obtient que f est affine sur des pavages du plan arbitrairement fin"
Comment obtient-on ça?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mai 2009, 23:40
par Nightmare » 11 Mai 2009, 23:40
Busard > Dans ta démo pour la conservation de

, tu parles du symétrique de O par rapport à quoi?
Plus simplement, deux points à distance

sont les sommets d'un losange de côté 1 !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
