^^ gros travail sur les congruences ^^
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 06 Juil 2009, 07:36
par Zavonen » 06 Juil 2009, 07:36
n peut-il être impair ? Que se passe-t-il si n est multiple de 4 ?
Répond déjà à ces deux questions très simples.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juil 2009, 07:36
par Dinozzo13 » 06 Juil 2009, 07:36
oui ! parce que
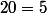
x
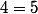
x
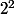
après ça nous donne :

x

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juil 2009, 07:40
par Dinozzo13 » 06 Juil 2009, 07:40
n ne peut pas être impair car le produit de n par n+6 est un nombre pair donc n est nécessairement pair.
Si n est multiple de 4 alors
=4k)
,
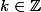
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 06 Juil 2009, 07:47
par Zavonen » 06 Juil 2009, 07:47
Si n est multiple de 4 alors n=4q
n(n+6) =16q²+24q = 8k
OK !
Donc il n'y a plus qu'à considérer le cas où n est un multiple de 2 sans être un multiple de 4, c'est à dire n=2q avec q impair.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juil 2009, 07:51
par Dinozzo13 » 06 Juil 2009, 07:51
en posant
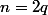
,

impair, je remplace et je trouve

, ce qui implique que

soit aussi pair
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 06 Juil 2009, 07:58
par Zavonen » 06 Juil 2009, 07:58
Tu cherches q impair tel que
2q(2q+6)=8k
soit après développement et simplification par 4
q(q²+3)=2k
comme q est impair il faut que q²+3 soit pair donc que q² soit impair donc que q soit impair.
En résumé.
les nombres n impairs ne sont pas solutions
Les nombres de la forme 2q avec q impair sont solutions
Les nombres de la forme 4q sont solutions
Au final les solutions sont les nombres pairs.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juil 2009, 08:02
par Dinozzo13 » 06 Juil 2009, 08:02
ça à l'air de concorder avec ce que j'ai trouvé non ?
(n,k)={
,(-2,-1),(-14,14),(-4,-1),(-8,2),(8,14))
}
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités