Question sur un exercice de DM
28 messages
- Page 1 sur 2 - 1, 2
Question sur un exercice de DM
Bonjour, j'ai un exercice à faire dans mon devoir maison et j'aurais souhaité si ce que je compte mettre est bon ou pas?
Données globales de l'exercice:
On appelle distance du point M à la droite D, la distance MH où H est le projeté orthogonal de M sur D.
D est la droite passant par A de vecteur normal v(=vecteur)n.
M est un point quelconque du plan et H est son projeté orthogonal sur D.
Dans le plan rapporté à un repère orthonormé (O ;i ;j), on suppose que D : ax+by+c=0, A(xa ;ya) et M(x ;y).
a. Démontrer que vAM.vn=ax+by+c
Indication : les coordonnées de A vérifient léquation de D.
Données globales de l'exercice:
On appelle distance du point M à la droite D, la distance MH où H est le projeté orthogonal de M sur D.
D est la droite passant par A de vecteur normal v(=vecteur)n.
M est un point quelconque du plan et H est son projeté orthogonal sur D.
Dans le plan rapporté à un repère orthonormé (O ;i ;j), on suppose que D : ax+by+c=0, A(xa ;ya) et M(x ;y).
a. Démontrer que vAM.vn=ax+by+c
Indication : les coordonnées de A vérifient léquation de D.
J'avais pensé mettre pour la question:
On sait que D est la droite passant par A de vecteur normal vn.
De plus, D: ax+by+c=0, A(xa;ya) et M(x;y).
D'où vn(a;b) et vAM(x-xa;y-ya).
Les coordonnées de A vérifient l'équation de D.
D'où vAM.vn=a(x-xa)+b(y-ya)
vAM.vn=a*x-a*xa+b*y-b*ya
Or D:ax+by+c=0
Donc c=-ax-by
vAM.vn=ax+by+c si et seulement si vAM.vn=0
D'où a*x-a*xa+b*y-b*ya=0
a*xa+b*ya=a*x+b*y
-a*xa-b*ya=-a*x-b*y
Or c=-ax-by
D'où vAM.vn=ax+by+c
On sait que D est la droite passant par A de vecteur normal vn.
De plus, D: ax+by+c=0, A(xa;ya) et M(x;y).
D'où vn(a;b) et vAM(x-xa;y-ya).
Les coordonnées de A vérifient l'équation de D.
D'où vAM.vn=a(x-xa)+b(y-ya)
vAM.vn=a*x-a*xa+b*y-b*ya
Or D:ax+by+c=0
Donc c=-ax-by
vAM.vn=ax+by+c si et seulement si vAM.vn=0
D'où a*x-a*xa+b*y-b*ya=0
a*xa+b*ya=a*x+b*y
-a*xa-b*ya=-a*x-b*y
Or c=-ax-by
D'où vAM.vn=ax+by+c
Salut
La rédaction est un peu confuse .
Exemple de rédaction :
Etablissons l'équation cartésienne de la droite D , perpendiculaire à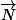 de coordonnées (a;b) et passant par A
de coordonnées (a;b) et passant par A )
Si la droite est perpendiculaire à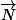 , alors , pour tout point P de coordonnées (x;y ) , de la droite D ,
, alors , pour tout point P de coordonnées (x;y ) , de la droite D , 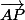 est orthogonal à
est orthogonal à 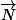
donc leur produit scalaire est nul
après avoir calculé le produit scalaire , tu dis :
donc l'équation cartésienne de la droite D est
 = 0)
donc si l'équation de la droite est
ax + by + c =0, alors)
La rédaction est un peu confuse .
Exemple de rédaction :
Etablissons l'équation cartésienne de la droite D , perpendiculaire à
Si la droite est perpendiculaire à
donc leur produit scalaire est nul
après avoir calculé le produit scalaire , tu dis :
donc l'équation cartésienne de la droite D est
donc si l'équation de la droite est
ax + by + c =0, alors
Le schéma est déjà fait avec l'exercice, en fait l'exercice est divisé en 2 partie.
Voilà le plan de l'exercice:
Tout d'abord avant la partie A il y a comme donnée :
On appelle distance du point M à la droite D, la distance MH où H est le projeté orthogonal de M sur D.
Ensuite il y a les questions de la partie A
Puis la partie B:
Les données sont alors:
D est la droite passant par A de vecteur normal v(=vecteur)n.
M est un point quelconque du plan et H est son projeté orthogonal sur D.
Puis il y a le schéma, le "1.Point de vue géométrique" avec deux question et le "2.Point de vue analytique" avec comme données:
Dans le plan rapporté à un repère orthonormé (O ;i ;j), on suppose que D : ax+by+c=0, A(xa ;ya) et M(x ;y).
Enfin il y a les questions de la partie 2 avec comme première question:
a. Démontrer que vAM.vn=ax+by+c
Indication : les coordonnées de A vérifient léquation de D.
J'ai juste marqué les données qui me sont données.
Voilà le plan de l'exercice:
Tout d'abord avant la partie A il y a comme donnée :
On appelle distance du point M à la droite D, la distance MH où H est le projeté orthogonal de M sur D.
Ensuite il y a les questions de la partie A
Puis la partie B:
Les données sont alors:
D est la droite passant par A de vecteur normal v(=vecteur)n.
M est un point quelconque du plan et H est son projeté orthogonal sur D.
Puis il y a le schéma, le "1.Point de vue géométrique" avec deux question et le "2.Point de vue analytique" avec comme données:
Dans le plan rapporté à un repère orthonormé (O ;i ;j), on suppose que D : ax+by+c=0, A(xa ;ya) et M(x ;y).
Enfin il y a les questions de la partie 2 avec comme première question:
a. Démontrer que vAM.vn=ax+by+c
Indication : les coordonnées de A vérifient léquation de D.
J'ai juste marqué les données qui me sont données.
Huppasacee a écrit:Salut
La rédaction est un peu confuse .
Exemple de rédaction :
Etablissons l'équation cartésienne de la droite D , perpendiculaire àde coordonnées (a;b) et passant par A
Si la droite est perpendiculaire à, alors , pour tout point P de coordonnées (x;y ) , de la droite D ,
est orthogonal à
donc leur produit scalaire est nul
après avoir calculé le produit scalaire , tu dis :
donc l'équation cartésienne de la droite D est
donc si l'équation de la droite est
ax + by + c =0, alors
L'équation cartésienne est trouvé par la relation AM.n=x_AM*x_n+y_AM*y_n ???
Par contre je voulais savoir si ce que j'ai mis pour les 2 premières questions (a et b) de la partie 2 est bon ou pas ?
http://maths-forum.com/showthread.php?t=85512&page=2
http://maths-forum.com/showthread.php?t=85512&page=2
donc voilà la consigne:
Distance dun point à une droite
On appelle distance du point M à la droite D, la distance MH où H est le projeté orthogonal de M sur D.
Partie A. Un premier exemple
(O,i,j) est un repère orthonormé du plan.
1. Tracer D : 2x-y+1=0 et placer M(1 ;2).
2. Déterminer une équation cartésienne de la droite déquation D1 perpendiculaire à D et passant par M et la tracer.
3. En déduire les coordonnées de H projeté orthogonal de M sur D puis calculer MH.
Partie B. Cas général
D est la droite passant par A de vecteur normal v(=vecteur)n.
M est un point quelconque du plan et H est son projeté orthogonal sur D.
1. Point de vue géométrique
a. Démontrer que vAM.vn=vHM.vn.
b. En déduire que d=|vAM.vn|/norme de vn.
2. Point de vue analytique
Dans le plan rapporté à un repère orthonormé (O ;i ;j), on suppose que D : ax+by+c=0, A(xa ;ya) et M(x ;y).
a. Démontrer que vAM.vn=ax+by+c
Indication : les coordonnées de A vérifient léquation de D.
b. En déduire que d=|ax+by+c|/racine de a²+b².
c. Retrouver le résultat de la partie A en utilisant cette formule.
Distance dun point à une droite
On appelle distance du point M à la droite D, la distance MH où H est le projeté orthogonal de M sur D.
Partie A. Un premier exemple
(O,i,j) est un repère orthonormé du plan.
1. Tracer D : 2x-y+1=0 et placer M(1 ;2).
2. Déterminer une équation cartésienne de la droite déquation D1 perpendiculaire à D et passant par M et la tracer.
3. En déduire les coordonnées de H projeté orthogonal de M sur D puis calculer MH.
Partie B. Cas général
D est la droite passant par A de vecteur normal v(=vecteur)n.
M est un point quelconque du plan et H est son projeté orthogonal sur D.
1. Point de vue géométrique
a. Démontrer que vAM.vn=vHM.vn.
b. En déduire que d=|vAM.vn|/norme de vn.
2. Point de vue analytique
Dans le plan rapporté à un repère orthonormé (O ;i ;j), on suppose que D : ax+by+c=0, A(xa ;ya) et M(x ;y).
a. Démontrer que vAM.vn=ax+by+c
Indication : les coordonnées de A vérifient léquation de D.
b. En déduire que d=|ax+by+c|/racine de a²+b².
c. Retrouver le résultat de la partie A en utilisant cette formule.
Et pour la question 1.a:
On sait que D est la droite passant par A de vecteur normal n, M est un point quelconque du plan et H est son projeté orthogonal sur D.
D'où [AH] est perpendiculaire à [HM].
Donc H est le projeté orthogonal de A sur [HM].
On sait que H est le projeté orthogonal de A sur [HM].
D'où vAM.n=vHM.n
On sait que D est la droite passant par A de vecteur normal n, M est un point quelconque du plan et H est son projeté orthogonal sur D.
D'où [AH] est perpendiculaire à [HM].
Donc H est le projeté orthogonal de A sur [HM].
On sait que H est le projeté orthogonal de A sur [HM].
D'où vAM.n=vHM.n
Il faut d'abord déterminer l'équation de la droite D1
Maintenant , prenons un point Q de D1 , de coordonnées ( x ; y )
si la droite D1 est perpendiculaire à D , comme D est perpendiculaire à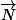 , alors D1 est parallèle à
, alors D1 est parallèle à 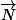
ce qui fait que est colinéaire à
est colinéaire à 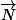
Il faut donc écrire la condition de colinéarité , faire le produit en croix , et trouver l'équation cartésienne de D1
Ensuite , tu écris l'équation de D sous la forme
y = mx + p ( équation réduite )
pareil pour D1
et comme H est le projeté orthogonal de M sur D , il est sur D et sur D1 , donc il faut calculer l'intersection de D et D1 pour trouver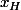 et
et 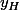
Maintenant , prenons un point Q de D1 , de coordonnées ( x ; y )
si la droite D1 est perpendiculaire à D , comme D est perpendiculaire à
ce qui fait que
Il faut donc écrire la condition de colinéarité , faire le produit en croix , et trouver l'équation cartésienne de D1
Ensuite , tu écris l'équation de D sous la forme
y = mx + p ( équation réduite )
pareil pour D1
et comme H est le projeté orthogonal de M sur D , il est sur D et sur D1 , donc il faut calculer l'intersection de D et D1 pour trouver
Huppasacee a écrit:Il faut d'abord déterminer l'équation de la droite D1
Maintenant , prenons un point Q de D1 , de coordonnées ( x ; y )
si la droite D1 est perpendiculaire à D , comme D est perpendiculaire à, alors D1 est parallèle à
ce qui fait queest colinéaire à
Il faut donc écrire la condition de colinéarité , faire le produit en croix , et trouver l'équation cartésienne de D1
Ensuite , tu écris l'équation de D sous la forme
y = mx + p ( équation réduite )
pareil pour D1
et comme H est le projeté orthogonal de M sur D , il est sur D et sur D1 , donc il faut calculer l'intersection de D et D1 pour trouveret
Ta réponse, c'est pour quelle question??
28 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
