Bonjour,
J'ai un DM, et je n'arrive pas à faire une démonstration.
Sphère circonscrite à un tétraèdre. [AB] est un segment et M est son milieu.
1.a.Démontrer que si N appartient au plan médiateur à [AB] alors NA = NB.
C'est une évidence, mais je ne sais pas comment le prouver. :s
J'ai pensé à un prendre un point N qui appartient au plan, du coup on a,
MNA et MNB triangles rectangles, donc avec pythagore, MA = MB, est-ce bon ?
2.La réciproque est-elle vraie ?
J'essaie en prenant des objets autour de moi (pour visualiser) de voir si oui ou non, ou si ça à l'air, mais je n'y arrive pas. Je bloque vraiment ici. Si vous avez une quelconque idée, je veux bien prendre.
Merci à vous.
DM Maths
8 messages
- Page 1 sur 1
Bonsoir,
1.a.Démontrer que si N appartient au plan médiateur à [AB] alors NA = NB.
C'est une évidence, mais je ne sais pas comment le prouver. :s
exact : il suffit de donner la définition du plan médiateur d'un segment...
2.La réciproque est-elle vraie ?
par définition...Mais jusque là on ne parle ni de tétraèdre, ni de sphère...
Très cordialement
1.a.Démontrer que si N appartient au plan médiateur à [AB] alors NA = NB.
C'est une évidence, mais je ne sais pas comment le prouver. :s
exact : il suffit de donner la définition du plan médiateur d'un segment...
2.La réciproque est-elle vraie ?
par définition...Mais jusque là on ne parle ni de tétraèdre, ni de sphère...
Très cordialement
Bonjour,
Je reconnais que mes définitions datent ...et que bien des choses ont changées pour faire entrer de force les mathématiques dans des programmes discutables...
Pour moi les mathématiques (on voulait aller bers la mathématique) unifiaient toute les définitions...
le plan médiateur dans l'espace avait la même définition que la médiatrice dans de plan etc...
don c'était l'ensemble des points de l'espace équidistants de A et de B...
mais j'ai déjà constaté que l'enseignement avait perdu de son exactitude (il y a un bout de temps quand mon IPR préférée a poussé un soupir de soulagement en prenant sa retraite, elle ne supportait plus les contorsions que l'on faisait aux math et d'être obligée de nous les transmettre !) à force de prendre de fausses définitions et de confondre des choses distinctes on finit par se perdre...
il y a tant de choses aberrantes enseignées aujourd'hui... et j'en découvre chaque jour de nouvelles !)
Ce que ces grands pontes ne voient pas c'est qu'en détruisant les bases de la formation, on arrive à des constructions bancales et une vision faussée des choses !.
Pardon pour cette digression, mais c'est qu'en tant d'années d'enseignement, j'en ai gros sur la "patate" !
Nightmare, je n'en ai nullement après toi, tu as simplement appliqué les élucubrations de programmes imbéciles!
Je me bats du côté de la jeunesse depuis mon choix de métier (par vocation pour l'enseignement et l'amour des math) ... ce que je fais ici n'en est que la suite logique, même si c'est parfois déphasé...
Très cordialement (et ce n'est pas ironique !)
PS : Pourrait-on me donner l'actuelle définition d'un plan médiateur ?
Je reconnais que mes définitions datent ...et que bien des choses ont changées pour faire entrer de force les mathématiques dans des programmes discutables...
Pour moi les mathématiques (on voulait aller bers la mathématique) unifiaient toute les définitions...
le plan médiateur dans l'espace avait la même définition que la médiatrice dans de plan etc...
don c'était l'ensemble des points de l'espace équidistants de A et de B...
mais j'ai déjà constaté que l'enseignement avait perdu de son exactitude (il y a un bout de temps quand mon IPR préférée a poussé un soupir de soulagement en prenant sa retraite, elle ne supportait plus les contorsions que l'on faisait aux math et d'être obligée de nous les transmettre !) à force de prendre de fausses définitions et de confondre des choses distinctes on finit par se perdre...
il y a tant de choses aberrantes enseignées aujourd'hui... et j'en découvre chaque jour de nouvelles !)
Ce que ces grands pontes ne voient pas c'est qu'en détruisant les bases de la formation, on arrive à des constructions bancales et une vision faussée des choses !.
Pardon pour cette digression, mais c'est qu'en tant d'années d'enseignement, j'en ai gros sur la "patate" !
Nightmare, je n'en ai nullement après toi, tu as simplement appliqué les élucubrations de programmes imbéciles!
Je me bats du côté de la jeunesse depuis mon choix de métier (par vocation pour l'enseignement et l'amour des math) ... ce que je fais ici n'en est que la suite logique, même si c'est parfois déphasé...
Très cordialement (et ce n'est pas ironique !)
PS : Pourrait-on me donner l'actuelle définition d'un plan médiateur ?
On me demande une équation de  plan médiateur à
plan médiateur à 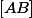 .
.
)
)
)
 est un vecteur normal à
est un vecteur normal à  .
.
Donc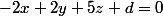 est une équation de
est une équation de  .
.
 milieu de
milieu de 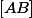 , d'où
, d'où ) (je ne suis pas sur du tout que ce soit les bonnes coordonnées :s).
(je ne suis pas sur du tout que ce soit les bonnes coordonnées :s).
Donc vérifie l'équation de
vérifie l'équation de  .
.
Alors,+d=0)
D'où
Pouvez-vous me dire si le raisonnement est bon ? Si les coordonnées de sont bonnes ? Et si l'équation de
sont bonnes ? Et si l'équation de  est bonne aussi ?
est bonne aussi ?
Merci à vous,
Donc
Donc
Alors,
D'où
Pouvez-vous me dire si le raisonnement est bon ? Si les coordonnées de
Merci à vous,
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
