Fonction régulière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 06 Fév 2009, 14:14
par legeniedesalpages » 06 Fév 2009, 14:14
Bonjour,
je voudrais montrer que la fonction
=e^{\frac{1}{x^2-1})
définie sur
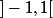
est dérivable à droite de 1, ainsi que toutes ses dérivées.
Pour
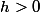
et suffisamment petit je trouve
-\rho(1-h)}{h} = -\frac{e^{ \frac{1}{h^2-2h} }}{h})
,
et lorsque je fais tendre

vers 0, je tombe sur une forme indéterminée que je n'arrive pas à lever.
Merci pour votre aide.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Fév 2009, 15:26
par Nightmare » 06 Fév 2009, 15:26
Salut :happy3:
As-tu fait une DES de ton exposant?
})
Ton taux de variation vaut donc :
}}}{h})
La première tend vers 1/2 et la deuxième tend vers l'infini... problème !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Fév 2009, 15:28
par Nightmare » 06 Fév 2009, 15:28
Aïe, la première ne tend pas vers 1/2, le h est au dénominateur, ça tend vers l'infini, forme indeterminée donc.
 par legeniedesalpages » 06 Fév 2009, 15:35
par legeniedesalpages » 06 Fév 2009, 15:35
Bonjour Jord,
en y réfléchissant je pensais plutôt utiliser les croissances comparées, j'essaie de développer mon raisonnement c'est pas clair du tout :hein:
Mais je n'avais pas du tout pensé à une DES.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Fév 2009, 15:36
par Nightmare » 06 Fév 2009, 15:36
Autre méthode donc, mise sous forme canonique :
On pose
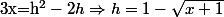
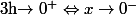
=-\frac{e^{\frac{1}{x}}}{1-\sqrt{x+1}})
On multiplie par la quantité conjuguée :
=\frac{e^{\frac{1}{x}}}{x}(1+ \sqrt{x+1}))
Or :
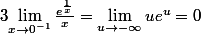
Finalement
 \longrightarrow_{x\to 0^{-}} 0)
:happy3:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 06 Fév 2009, 16:50
par ThSQ » 06 Fév 2009, 16:50
Tiens le retour de la fonction infiniment plate (aka la super-glu C°°

) !
Pour simplifier on ramène le pb en 0 : il suffit de montrer que
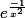
est C°° (et à toutes ses dérivées nulles en zéro).
Lemme : f : [a, b] -> R C°, dérivable sur [a, b] sauf en c avec a c. Alors f est dérivable en c et on a f'(c) = l.
Un coup de TAF. + généralisation à
})
Maintenant : par réc
}(x) = e^{\frac{-1}{x^2}} Q_n(x))
avec
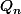
une fraction rationnelle. + lemme
-
Black Jack
 par Black Jack » 06 Fév 2009, 17:36
par Black Jack » 06 Fév 2009, 17:36
Question à 100 sous :
Est-il normal d'essayer de montrer qu'une fonction définie par hypothèse sur ]-1 ; 1[ est dérivable à DROITE de 1 ?
:zen:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Fév 2009, 17:39
par Doraki » 06 Fév 2009, 17:39
Moi aussi ça me perturbe ! Elle l'est trivialement parcequ'il n'y a rien à vérifier !
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 06 Fév 2009, 18:36
par ThSQ » 06 Fév 2009, 18:36
Elle serait pas vaguement prolongeable en +-1 des fois ....
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 06 Fév 2009, 19:29
par xyz1975 » 06 Fév 2009, 19:29
legeniedesalpages a écrit:Bonjour,
je voudrais montrer que la fonction
=e^{\frac{1}{x^2-1})
définie sur
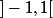
est dérivable à droite de 1, ainsi que toutes ses dérivées.
Pour
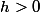
et suffisamment petit je trouve
-\rho(1-h)}{h} = -\frac{e^{ \frac{1}{h^2-2h} }}{h})
,
et lorsque je fais tendre

vers 0, je tombe sur une forme indéterminée que je n'arrive pas à lever.
Merci pour votre aide.
Une façon équivalente à celle donnée par Nightmare :
On multiplie et on divise par h-2 :
[ \frac{e^{ \frac{1}{h^2-2h} }}{h(h-2)}])
La quantité entre crochets se rapproche de 0, pour le voir il suffit de poser
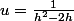
On peux aussi utiliser les équivalences mais c'est long.
-
Black Jack
 par Black Jack » 06 Fév 2009, 19:58
par Black Jack » 06 Fév 2009, 19:58
Il me semble bizarre de chercher si une fonction définie sur ]-1 ; 1[ est dérivable à droite de 1... Donc là où elle n'est pas définie.
Si on veut essayer de prolonger la fonction en +1, on peut mais il s'agit alors d'une autre fonction...
Et de toute manière : lim(x -> +1-) [e^(1/(x²-1))] = 0 et lim(x -> +1+) [e^(1/(x²-1))] = +oo et donc ...
Mais je ne suis pas mathématicien.
:zen:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 06 Fév 2009, 23:35
par kazeriahm » 06 Fév 2009, 23:35
en fait c'est un exemple de fonction assez connu et utile en théorie des distributions.
on montre que la fonction f définie par x->e^(1/x^2-1) sur ]-1,1[ et 0 partout ailleurs est C infini (et bien sur à support compact), ce qui constitue une bonne base pour étudier les distributions, qui sont les formes linéaires continues sur l'ev des fonctions c infini à support compact.
 par legeniedesalpages » 07 Fév 2009, 11:38
par legeniedesalpages » 07 Fév 2009, 11:38
oui je voulais bien entendu dire à gauche de 1 :briques:
J'avais pensé au lemme, mais pas au TAF.
Merci à vous.
 par legeniedesalpages » 07 Fév 2009, 11:40
par legeniedesalpages » 07 Fév 2009, 11:40
kazeriahm a écrit:en fait c'est un exemple de fonction assez connu et utile en théorie des distributions.
on montre que la fonction f définie par x->e^(1/x^2-1) sur ]-1,1[ et 0 partout ailleurs est C infini (et bien sur à support compact), ce qui constitue une bonne base pour étudier les distributions, qui sont les formes linéaires continues sur l'ev des fonctions c infini à support compact.
Effectivement, c'est dans ce contexte que je suis tombé sur cette fonction.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
définie sur
est dérivable à droite de 1, ainsi que toutes ses dérivées.
et suffisamment petit je trouve
,
vers 0, je tombe sur une forme indéterminée que je n'arrive pas à lever.