Représentation régulière

[mashke]

Bonjour,

Je commence les représentations linéaires et j'ai une question basique :
Pourquoi la représentation régulière à droite est une représentation ?
En mathématiques, ca veut dire :
Pour et des groupes ;
avec .
Alors f est une reprsentation linéaire.

Cordialement ,
Mashke

[Skullkid]

Bonjour, tu te trompes sur la définition de la représentation régulière à droite (enfin, formellement elle est correcte mais vu les notations que tu as choisies, y a un souci). Dans les cas comme ça où on est amené à manipuler des fonctions de fonctions de fonctions, une bonne habitude à prendre est de commencer par bien définir tous les objets, en particulier écrire noir sur blanc qui est une fonction de quoi dans quoi :

G est un groupe, K est un corps. La représentation régulière à droite c'est une certaine fonction r de G dans Aut(K^G), définie par . En décortiquant la définition :

- g et h sont des éléments de G
- f est une fonction de G dans K
- est une fonction de K^G dans lui-même
- est une fonction de G dans K
- est un élément de K

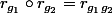
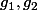
Pour vérifier que r est bien une représentation, on doit vérifier que pour tous dans G. Qu'est-ce que ça donne quand tu "déballes" la définition de et ?

[mashke]

Bonjour,

On obtient :

Mais ne peut etre donnée, non ?
D'ailleurs , nous sommes pas censés "casser" ?

Cordialement,
Mashke

[Skullkid]

Puisque tu as la définition de et tu peux calculer leur composée ! Après, en effet tu peux choisir de partir de et le "casser" pour arriver à , ou d'aller dans l'autre sens, c'est comme tu préfères. Ce que j'ai suggéré dans mon post est en fait un compromis entre les deux (au lieu d'écrire une série d'égalités A = ... = B ou B = ... = A, on écrit A = ... = C et B = ... = C) que j'ai tendance à trouver plus facile, mais c'est une question de goût.

[mashke]

Mais je trouve étrange qu'on est aucune information sur f. Ce n'est pas un homormorphisme, comment suis-je censé le casser ?
Mais je vais essayer votre méthode ;

Cordialement,
Mashke

[Skullkid]

En effet tu ne sais rien sur f. Tout ce que tu as à disposition c'est la définition de r, avec laquelle il va falloir jongler.

Pour te mettre sur la voie, tu peux remarquer que .

[mashke]

Alors j'obtiens :

mais
d'où .

[Skullkid]

C'est ça. Après comme les notions sont encore nouvelles pour toi, et que ce que tu veux montrer revient uniquement à écrire les définitions, je pencherais vers une rédaction hyper détaillée. Là tel que tu l'as écrit ça fait un peu tour de passe-passe.

Une démonstration qui ne passe aucune étape sous silence (et donc trop "lourde" pour quelqu'un de familier avec les notions employées) serait quelque chose comme :

avec . Donc en appliquant la définition de , . Maintenant on peut poser , ce qui donne par définition de . D'où finalement .

[mashke]

En effet, ma démonstration est brouillon.
Votre démonstration est claire et précise.
Merci du conseil et de votre aide,

Cordialement;
Mashke