Arithmétique - PGCD
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Blenno
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Oct 2007, 12:45
-
 par Blenno » 11 Jan 2009, 14:49
par Blenno » 11 Jan 2009, 14:49
Bonjour.
n est un entier naturel supérieur ou égal à 2.
1.Montrer que n et 2n+1 sont premiers entre eux.
On cherche donc à montrer que pgcd(n;2n+1)=1
J'ai débuté comme ceci:
On a d, tel que pgcd(n;2n+1)=d.
D'où d|n.
D'où d|2n.
On a d|2n+1, donc (par soustraction) d|1
Donc d=1 (car d est un pgcd, et un pgcd est un entier).Ce que j'ai fais, est-ce bon ?
Merci d'avance.

-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 11 Jan 2009, 14:51
par XENSECP » 11 Jan 2009, 14:51
Bah l'algo d'Euclide permet de conclure directement mais ouais c'est bon ;)
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 11 Jan 2009, 14:58
par guigui51250 » 11 Jan 2009, 14:58
J'aurais plutot utilisé Bezout pour montrer ça :
dire que a et b sont premiers entre eux équivaut à dire qu'il existe u et v entiers tels que au+bv=1, pour u=-2 et v=1 ça marche donc a et b premiers entre eux
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 11 Jan 2009, 15:02
par ft73 » 11 Jan 2009, 15:02
+1 pour Euclide, c'est la solution la plus élégante.
Mais tout le reste marche aussi, tout va bien !
-
Blenno
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Oct 2007, 12:45
-
 par Blenno » 11 Jan 2009, 15:07
par Blenno » 11 Jan 2009, 15:07
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 11 Jan 2009, 15:12
par ft73 » 11 Jan 2009, 15:12
si tu divises alpha et beta, alors tu divises 2*alpha-beta... etc...
-
Blenno
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Oct 2007, 12:45
-
 par Blenno » 11 Jan 2009, 15:15
par Blenno » 11 Jan 2009, 15:15
J'ai fais comme ceci (j'avais pas pensé):

et

d'où

d'où

Donc

.

.
Edit: Le soucis, c'est qu'on mettre d'autres coefficients.
Genre 3\alpha-\beta, etc....

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Jan 2009, 15:20
par leon1789 » 11 Jan 2009, 15:20
ft73 a écrit:+1 pour Euclide, c'est la solution la plus élégante.
Mais tout le reste marche aussi, tout va bien !
Personnellement, je préfère utiliser tout simplement la définition du pgcd (cf message 1) ou Bezout (cf message 3), c'est moins lourd que l'algo d'Euclide dans toute sa généralité (surtout quand le déroulement de l'algo s'arrête à la première division euclidienne, peut-on parler d'application de l'algorithme d'Euclide ?...)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Jan 2009, 15:24
par leon1789 » 11 Jan 2009, 15:24
Blenno a écrit:J'ai fais comme ceci (j'avais pas pensé):

et

d'où

d'où

Donc

.
oui, ici encore, c'est simplement la définition (et encore !) du pgcd qu'on utilise. :+:
Blenno a écrit:
.
heu pourquoi ?
Blenno a écrit:Edit: Le soucis, c'est qu'on mettre d'autres coefficients.
Genre 3\alpha-\beta, etc....
oui, et cela conduit-il à des conclusions intéressantes ?
-
Blenno
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Oct 2007, 12:45
-
 par Blenno » 11 Jan 2009, 15:30
par Blenno » 11 Jan 2009, 15:30
leon1789 a écrit:heu pourquoi ?

Donc

Donc

(ou
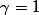
?).
leon1789 a écrit:oui, et cela conduit-il à des conclusions intéressantes ?
Intéressantes ? Je n'sais pas.
Mais pour le cas

On a

.
Ce qui est plutôt différent de

.
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 11 Jan 2009, 15:30
par ft73 » 11 Jan 2009, 15:30
leon1789 a écrit:Personnellement, je préfère utiliser tout simplement la définition du pgcd (cf message 1) ou Bezout (cf message 3), c'est moins lourd que l'algo d'Euclide dans toute sa généralité (surtout quand le déroulement de l'algo s'arrête à la première division euclidienne, peut-on parler d'application de l'algorithme d'Euclide ?...)
Ok pour la méthode "manuelle", mais pas pour Bézout, je ne trouve pas le th. de Bézout plus simple qu'Euclide... Peut-on parler d'application du th. de Bézout aussi ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Jan 2009, 15:37
par leon1789 » 11 Jan 2009, 15:37
Blenno a écrit:
Donc

Donc

(ou
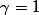
?).
oui,

ou
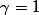
Ne pas abandonner l'une des deux possibilités :id:
Blenno a écrit:Intéressantes ? Je n'sais pas.
Mais pour le cas

On a

.
Ce qui est plutôt différent de

.
Oui, et cela te pose problème d'arriver à deux gâteaux différents en suivant deux recettes différentes ?
Remarque que la recette de ton exo

produit un gâteau plus gouteux

que ton essai

pour arriver à un "énigmatique"

.
Non ?
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 11 Jan 2009, 15:38
par ft73 » 11 Jan 2009, 15:38
...d'autant que je connais ce pb de bac et il n'y est pas question de 3*alpha-beta !!

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Jan 2009, 15:41
par leon1789 » 11 Jan 2009, 15:41
ft73 a écrit:Ok pour la méthode "manuelle", mais pas pour Bézout, je ne trouve pas le th. de Bézout plus simple qu'Euclide... Peut-on parler d'application du th. de Bézout aussi ?
Bézout, c'est : pgcd(a,b)=1 ua+vb = 1
En fait la partie intéressante de ce résultat (ce que l'on peut réellement appeler le théorème de Bezout), c'est pgcd(a,b)=1 => ua+vb = 1
Ici dans l'exo, on utilise l'implication réciproque qui est "évidente" (because définition). Dire que c'est du Bézout, c'est un peu abuser, ok.
-
Blenno
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Oct 2007, 12:45
-
-
Blenno
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Oct 2007, 12:45
-
 par Blenno » 15 Jan 2009, 17:40
par Blenno » 15 Jan 2009, 17:40
Je trouve toujours pas, mais bon,
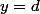
, donc
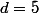
ou
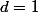
.
Question suivante:
En déduire le


, de

et

en fonction de

.
Là j'dois avouer que j'arrive à rien. :doh: :dodo:
-
Blenno
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Oct 2007, 12:45
-
 par Blenno » 15 Jan 2009, 18:29
par Blenno » 15 Jan 2009, 18:29
J'avais fais une erreur de calcul à la question 3, donc ça me bloquait ici ^^. Le DM est terminé, merci à vous. ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
