[MPSI] Dévelopement limités
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 12 Jan 2006, 18:47
par Gnörf » 12 Jan 2006, 18:47
Bonsoir à tous!
Voilà, j'aimerai savoir s'il est possible de se servir des developement limités dans un calcul de limite. Je n'ai pas encore fait le cour mais le prof nous a donné certaines formules et j'ai plusieurs limites à calculer pour demain. La vraie question est de savoir si l'on peut s'en servir dans des additions et soustractions (le probleme des équivalences était justement là : il fallait se limiter aux multiplications et quotients). Voila donc comment j'ai procédé pour calculer une limite qui m'était demandé:

En se servant de la formule
^\alpha = x\alpha+1+o(x))
(en zéro).
On a
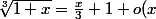)
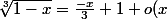)
(<- Si une fonction g(x)=
)
alors g(x)=
)
???)
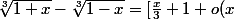] - [\frac{-x}{3}+1+o(x)])
)

D'ou enfin:

Si quelque chose ne vas pas j'aimerai bien savoir pourquoi ... je vous remercie tous et a bientot !
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 12 Jan 2006, 18:50
par Galt » 12 Jan 2006, 18:50
La réponse est que oui, on peut et même que c'est rudement une bonne méthode. Dans tes DL, toutefois, mets le terme le plus grand (donc ici le terme constant 1) en premier.
Après tout, en première approximation, quand x est voisin de 0,
^{\frac 1 3})
est quand même voisin de 1.
Bonne continuation
Galt
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 12 Jan 2006, 18:52
par Gnörf » 12 Jan 2006, 18:52
Merci beaucoup !!! Je sens que je vais adorer les développements limités
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 12 Jan 2006, 18:55
par Galt » 12 Jan 2006, 18:55
Une dernière remarque : ton calcul est juste, mais tu a mis un équivalent à la fin. C'est OK, il n'y a pas ici de problème, mais souviens toi : ON NE PEUT PAS AJOUTER OU SOUSTRAIRE DES EQUIVALENTS
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 12 Jan 2006, 19:11
par Gnörf » 12 Jan 2006, 19:11
Juste à propos des equivalents, ai je le droit de les passer sous racine: est-ce que

je sais que l'on ne peut les composer avec des fonctions comme exponentielle mais racine ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Jan 2006, 19:24
par Pythales » 12 Jan 2006, 19:24
Attention. Si x tend vers zéro, rac(x^2+x) est équivalent à rac(x). Si x tend vers l'infini, rac(x^2+x) est équivalent à valeur absolue de x.
-
Gnörf
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Jan 2006, 18:09
-
 par Gnörf » 12 Jan 2006, 19:35
par Gnörf » 12 Jan 2006, 19:35
Donc en faite si j'ai par exemple (en zéro)

J'ai :

je ne peut pas dire

?
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 12 Jan 2006, 20:03
par Galt » 12 Jan 2006, 20:03
Tu peux presque le dire
En 0,
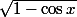
est équivalent à
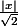
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 12 Jan 2006, 20:06
par Galt » 12 Jan 2006, 20:06
D'une manière intuitive, a est équivalent à b si
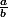
tend vers 1. Dans ce cas,

tend aussi vers 1 (ce ne serait pas le cas avec des exponentielles si a et b tendent vers l'infini, ni des ln si a et b tendent vers 1) donc
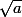
et
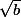
sont bien équivalents
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
