Dévelopement asymptotique

[sissou3409]

Bonjour,

J'aimerai savoir comment on fait pour trouvé une asymptote grâce au developpement limité.
Par exemple si on a y= x² arctan (1/x+1)

J'ai regardé dans des livres on me dit de posé h=1/x et de multiplié mon y par 1/abs(h), mais je comprend pas bien le but de cette méthode ni d'ailleur si je les bien comprise ^^

Merci

[nuage]

Salut,
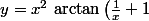je suppose que car si il n'y a pas d'asymptote.
On pose ensuite et on utilise le DL de arctan en zéro :
En remplaçant par on a :

[sissou3409]

Et donc l'asymptote et y=x-1.. Mais le devellopement limité de artan(h) n'est pas bon je crois.. ce ne serait pas plutot arctan(h)= ?

Merci, et dsl pr l'oublie de parenthèse mais tu a pris la bonne fonction!

[nuage]

Mais le devellopement limité de artan(h) n'est pas bon je crois.. ce ne serait pas plutot arctan(h)= ?

Non.
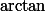
En principe, pour u voisin de zéro, mais comme est impaire on a un

Au passage dans le terme en est inutile. Tu donnes un DL à l'ordre 2.

[sissou3409]

Oki merci.

Donc maintenant si je cherche la même chose pour:


On pose x= h +1 et on utilise le DL de ln(1+h) en 0:


Ensuite en remplaçant, h par x-1, on a:

D'ou

Et l'asymptote serait donc y=3x/2 ?

[nuage]

on a et donc
au voisinage de plus l'infini.
Dans ce cas il n'est pas utile d'utiliser un DL.

[alavacommejetepousse]

Non.
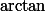
En principe, pour u voisin de zéro, mais comme est impaire on a un

Au passage dans le terme en est inutile. Tu donnes un DL à l'ordre 2.

la dérivée d arctan est f ' (x) =1/(1+x^2)

de dl
f'(x) = 1 -x^2 +0(x^3) donc par intégration le dl de f est

f (x) = 0 + x- x^3/3 +0(x^4)

[nuage]

la dérivée d arctan est f ' (x) =1/(1+x^2)

de dl
f'(x) = 1 -x^2 +0(x^3) donc par intégration le dl de f est

f (x) = 0 + x- x^3/3 +0(x^4)

Comme f est impaire, le terme de degré 4 est nul et f (x) = 0 + x- x^3/3 +0(x^5)

A+

[alavacommejetepousse]

certes

mais c est bien - x^3/3


et grand O de x^5 ou petit O de x^4 comme je l'ai écrit

[nuage]

certes

mais c est bien - x^3/3

Oui, j'ai fait une faute de frappe

et grand O de x^5 ou petit O de x^4 comme je l'ai écrit

Ce n'est pas ce que j'ai lu dans ton message de 23h00

f (x) = 0 + x- x^3/3 +0(x^4)

Mais tu peux encore le modifier.

[alavacommejetepousse]

heu que lis tu donc ?

[nuage]

heu que lis tu donc ?

Bonne question. En ce qui concerne cette discussion, je lis ce que tu as écrit.
Et il est bien connu que la confusion o 0 O est fréquente.

[alavacommejetepousse]

heu

je n ai nulle envie de polémiquer
je rectifiais l erreur de signe puisque c'était la question de sissou

pour la notation de landau on écrit tjrs a priori un petit 0 dans un dl

mais quand bien même j'aurais écrit un grand 0 que l'expression serait correcte

[nuage]

...
je rectifiais l erreur de signe...

Et je t'en remercie.

[sissou3409]

Pas besoin de se disputé pour une erreur de signe ^^

Merci en tout cas pour vos réponse! Si j'ai bien compris, ya pas de méthode systématique à utilisé, sa depend de la fonction en fait! Je suis pas sorti de l'auberge.. mdr :stupid_in

[kasarus]

Bonsoir,
je pose e (x) = x-3 pour faire le D.A.
Jusque là, aucun souci.
Ma question est:
Vu que l'ordre demandé pour le D.A est 2, comment fait on?
c'est l'ordre en e (x) qui doit être de deux ou l'ordre en x^2 (et là.. :doh: )

Je trouve comme résultat:

ln x = ln 3 - 2 + x - x^2 / 9
3
(en fait, je me pose la question: Manquerait-il des termes en x^2..)
Voilà.

[kasarus]

juste pour up un peu :help: