Exercice plaque homogène

[roxygirls]

Bonsoir ,
je dois rendre un exercice pour samedi mais je ne sais pas comment le résoudre est-ce que quelqu'un peut m'aider s'il vous plait ?

On considére une plaque homogène constituée d'un carré de côté a et de 4 triangles isocèles de côté a et rac2/2 a , le tour de même épaisseur .
On enléve la partie de la plaque constituée du triangle ABE.
Déterminer le centre d'inertie G de la plaque ainsi obtenue.

Merci d'avance

[phryte]

Bonjour.
Soit M le centre de gravité du triangle ABE.

Or EM = 2/3(a/2)
.....

[Florélianne]

Bonjour,
Si j'ai bien compris ton problème, en partant du carré ABCD on a crée un nouveau carré EFGH de côté aV2 sont les points A, B, C et D sont les milieux des côtés. Ensuite on a enlevé le triangle ABE.
Tu as que OF=OG=OH = a
Pour trouver ton centre d'inertie il faut chercher le barycentre des quatre centres d'inertie restants avec les masses correspondantes à leur surface : a² pour le carré , 1/2(a)(a/2)=a²/4 pour chacun des trois triangles ou en simplifiant par a² , 1 pour le carré et 1/4 pour les triangles
Soient I, J et K les centres d'inertie des triangles CBF , CDG et ADH , tu sais que FI* = (2/3)1/2 FO* = 1/3 FO*
de même GJ* = 1/3 GO* et HK* = 1/3 HO*
O étant le centre d'inertie de ABCD
Appelons Q le centre d'inertie de ta plaque
tu as : QO* + 1/4 QI*+1/4QJ*+1/4QK* = 0*
je te laisse finir, tu as tout ce dont tu as besoin...
Très cordialement

[roxygirls]

Bonjour,
merci de votre réponses mais je ne comprend pas ce que je dois faire pour la suite :/ pouvez-vous s'il vous palit m'expliquer ?
merci d'avance

[roxygirls]

?? Besoin d'aide s'il vous plait :/ je suis complétement perdu :'(

[phryte]

Bonjour.
En calculant GE tu as la position de G !

[roxygirls]

4*GE-1/4FGM=0
4*GE-1/4GE-1/4EM=0
15/4GE=1/4EM
or EM=2/3 (a/2)


GE est a 15/4 de EM non ?

Mias je ne sias pas comment démontrer que c'est le centre d'inertie :/

[phryte]

Bonsoir.

GE est a 15/4 de EM non ? Mias je ne sias pas comment démontrer que c'est le centre d'inertie :/

Non
GE=EM/15=a/(3*15)
G est le cdg puisque on a écrit sa relation vectorielle de définition : 4*GE-1/4GM=0

[roxygirls]

Mais pourquoi vous m'aviez écrit :
or EM=2/3 (a/2)

Merci de votre aide

[roxygirls]

Mais comment prouver que c'est le centre d'inertie ?

Merci

[phryte]

EM=2/3 (a/2)

M est le cdg du triangle ABE donc situé au 2/3 de sa hauteur à partie du point E.
Et sa hauteur esr égale à "a/2".

[roxygirls]

Bonjour,
oui je suis d'accord mais sa me permet pas de déterminer le centre inertie g de la plaque ainsi obtenue ?
c'est sa que je dois chercher et je n'y arrive pas :(
merci d'avance

[phryte]

Mais comment prouver que c'est le centre d'inertie ?

Car on a appliqué la formule :
Si G est le cdg du carré alors :
alpha*GE+beta*GM=0

[roxygirls]

D'accord merci beaucoup :
et la démonstration c'est :
4*GE-1/4GM=0
4*GE-1/4GE-1/4EM=0
15/4GE=1/4EM
or EM=1/3(a/2)
GE=EM/15=(a/3*15)

G est le centre de gravité puisque on a écrit sa relation vectorielle de définition = 4 * GE-1/4 GM=0

M est le centre de gravité du triangle ABE donc situé au 2/3 de sa hauteur à partir du point E et sa hauteur est égale à a/2

Et ayant appliqué la formule :
Si G est le cdg du carré alors :
alpha*GE+beta*GM=0

Nous pouvons alors dire que G est le centre d'inertie

Est-ce qu'il y a des erreurs dans ce que j'ai résumer ou pas ?!

merci beaucoup de votre aide :happy2:

[roxygirls]

est-ce qu'il y a des erreurs ?
merci

[phryte]

Bonjour.
Excuse moi j'ai fais une erreur ci-dessus.
Il faut écrire :
Soit M le centre de gravité du triangle ABE.
Soit P le poids de la plaque.

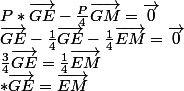
Or EM = 2/3(a/2)
Donc :
GE=a/9

Tu corriges
G est le centre de gravité puisque on a écrit sa relation vectorielle de définition = P* GE-P/4 GM=0
(Tu peux mettre a^2 à la place de P)

[roxygirls]

Donc tout cela suffit pour répondre a ma question ou je dois faire autre chose ?

je rajoute également
Et ayant appliqué la formule :
Si G est le cdg du carré alors :
alpha*GE+beta*GM=0

Nous pouvons alors dire que G est le centre d'inertie ??
merci d'avance

[phryte]

Bonjour.

je rajoute également Et ayant appliqué la formule : Si G est le cdg du carré alors : alpha*GE+beta*GM=0

Tu peux dire :
E étant le barycentre (cdg) de la plaque pleine et M celui du triangle ABE, le barycentre G de la plaque sans le triangle ABE satisfait l'équation :

[roxygirls]

Oui mais sa justifie que g est le centre d'inertie ?

[phryte]

Bonjour.

Oui mais sa justifie que g est le centre d'inertie ?

C'est la même chose :
- Centre d'inertie
- Barycentre
- Centre de gravité