[tout niveau] Question de limite ...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fritoman
- Messages: 5
- Enregistré le: 01 Jan 2006, 19:16
-
 par fritoman » 01 Jan 2006, 23:28
par fritoman » 01 Jan 2006, 23:28
Re-bonsoir à tous ...
vous n'en verez certainement pas l'utilité mais il m'est venu la question suivante :
L'égalité suivante est vraie ?
=\pi \times 10^n)
Bonne réflexion et merci encore
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Jan 2006, 23:33
par Nightmare » 01 Jan 2006, 23:33
Bonsoir
Non bien sûr que non, la partie entière comme son nom l'indique ne prend que des valeurs entières, comment voudrais-tu que sa limite soit un irrationnel ?
Rappelles toi que x < E(x) < x+1
:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Jan 2006, 23:41
par Nightmare » 01 Jan 2006, 23:41
Oui oui rain, je n'avais juste pas le courage de mettre le signe en latex :smoke:
-
Chimerade
- Membre Irrationnel
- Messages: 1472
- Enregistré le: 04 Juil 2005, 13:56
-
 par Chimerade » 01 Jan 2006, 23:49
par Chimerade » 01 Jan 2006, 23:49
fritoman a écrit:Re-bonsoir à tous ...
vous n'en verez certainement pas l'utilité mais il m'est venu la question suivante :
L'égalité suivante est vraie ?
=\pi \times 10^n)
Bonne réflexion et merci encore
Ceci est une expression incorrecte : une limite est un nombre ;

est une fonction de n.
Par contre tu pourrais écrire :
-\pi \times 10^n = 0)
...qui serait une expression correcte, au sens de la syntaxe, mais fausse, puisque l'expression
-\pi \times 10^n)
n'a pas de limite...
A la rigueur, on peut raisonner sur le fait que :
}{\pi \times 10^n} = 1)
qui elle serait à la fois correcte sur le plan de la syntaxe, et vraie...Je te laisse ce soin, si le coeur t'en dit...
-
fritoman
- Messages: 5
- Enregistré le: 01 Jan 2006, 19:16
-
 par fritoman » 02 Jan 2006, 00:48
par fritoman » 02 Jan 2006, 00:48
Merci pour vos réponse, je me suis rendu compte que ce que j'ai ecrit est absurde et faux . Cette question m'était en faite venue en cherchant une suite extraite de la suite

qui convergerait vers 0 avec:
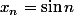
La suite extraite imaginé aurait été la suivente :

avec
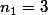
**
 : 3 \times 10^0)
**
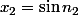
avec
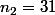
**
 : 3.1 \times 10^1)
**
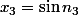
avec
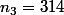
**
 : 3.14 \times 10^2})
**
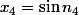
avec
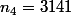
**
 : 3.141 \times 10^3)
**
...
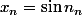
avec
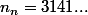
**
 : 3.141 \times 10^{n-1})
Cette suite extraite convergerai-t-elle vers 0 ? (ma réponse serait oui ... mais je ne suis qu'un novice en la matière)
Merci beaucoup :we: Je m'excuse d'avance pour les erreurs de TeX que j'ai pu faire, mais je commence a peine.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Jan 2006, 10:11
par yos » 02 Jan 2006, 10:11
Bonjour.
Je ne vois aucune raison pour qu'elle converge vers 0. Pour que ça marche il faut que l'indice n (ou plutôt phi(n)) de la suite extraite, se rapproche de l'ensemble piZ (ensemble des kpi avec k entier). On parle de convergence vers 0 modulo piZ.
Pour donner un exemple de cette convergence modulo un ensemble, il y a (
^n)
qui diverge vers

, mais qui converge vers 0 modulo Z (-->calculette). Il y a aussi les suites n!e et

.
A partir de ces exemples, je te laisse fabriquer une suite
)
d'entiers qui converge vers 0 modulo piZ (et donc telle que
)
converge vers 0.
-
Anonyme
 par Anonyme » 07 Jan 2006, 20:29
par Anonyme » 07 Jan 2006, 20:29
je suis un peu naze en maths mais cette limite ne tend pas vers +oo ?
-
shtefi
- Membre Naturel
- Messages: 46
- Enregistré le: 09 Juil 2005, 17:56
-
 par shtefi » 08 Jan 2006, 00:54
par shtefi » 08 Jan 2006, 00:54
Sans démonstration je dirais que cette limite est fausse car la partie entière de "pi"x10EXPn ne peut être "pi" aussi grand que soit n !!!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Jan 2006, 11:01
par yos » 08 Jan 2006, 11:01
Non inscrit* a écrit:... mais cette limite ne tend pas vers +oo ?
Une limite est un nombre ou +/- infini, et donc elle ne tend vers rien du tout. On peut dire :
"la SUITE tend vers +oo "
ou bien :
"la limite EST +oo ".
Si on veut faire des maths, il faut accepter que les mots aient un sens.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités