Chaine de markov
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
stitch
- Membre Naturel
- Messages: 74
- Enregistré le: 15 Oct 2006, 17:43
-
par stitch » 08 Nov 2008, 11:51
bonjour,
je suis sur une demonstration, et il y a une étape que j'ai du mal a comprendre. :hum:
voici les notations :
l'espace d'etat.
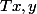
temps minimum pour aller a y a partir de x.
et voici l'equation que je ne comprends pas vraiment :
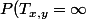=\sum_{x_1,...,x_n \in M \mid y} P(T_{x,y}={\infty}\mid X_{1}=x_1,...,X_{n}=x_n)P(X_{1}=x_1,...,X_{n}=x_n))
à la limite s'il n y avait pas de somme j'aurais trouvé ça plus parlant ...
quelqu'un a t il une idée ?
Merci beaucoup.
Bonne journée.
Stitch
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 08 Nov 2008, 14:59
Salut stitch,
si j'ai bien compris, ta somme se fait avec les
.
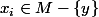
Si
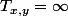
alors nécessairement
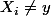
pour tout
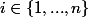
et donc
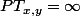=P\((T_{x,y}=\infty)\bigcup_{x_1,...,x_n\in M-\{y\}}(X_1=x_1,..., X_n=x_n)\))
en effet puisque
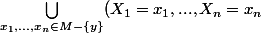\subset \{T_{x,y}=\infty\})
.
Donc,
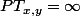=P\(\bigcup_{x_1,...,x_n\in M-\{y\}}T_{x,y}=\infty\cap(X_1=x_1,..., X_n=x_n)\)\\ \qquad\qquad=\sum\limits_{x_1,...,x_n\in M-\{y\}}P\(T_{x,y}=\infty\cap(X_1=x_1,..., X_n=x_n)\))
car l'union est disjointe.
Reste ensuite à utiliser la petite formule de proba conditionnelle :
=\frac{P\(A\cap B\)}{P(B)})
pour obtenir ce que tu cherches...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
