bonjours, je suis completement larguer sur cette exercice, pouvez vous m'aider mercie et me corriger.
On considere, dans un plan complexe, les points M,M',A,B d'affixes respectives z=x+iy, z'=x'+iy', za=2-2i et zb=-i
De plus on pose z'=f(z)=(z-za)/(i(z-zb))
1) determiner les antécédents par f de i et -i.
1) Il suffit de calculer f(z)=i et f(z)=-i; j'ai trouver que les antécédents de i est l'intersection de deux droites y=-3/2 et x=1.Et l'antécédants de -i est le point M(-2;1)
2) Par une méthode géométrique, déterminer l'ensemble E1 des points M tels que z' soit de module 1.
2)|z'|=1
|(z-zA)/i(z-zB)|=|z-zA|/|z-zB|=1
|z-zA|=|z-zB|
cela signifie que la distance de M à A est égale à la distance de M à B
donc l'ensemble des points M est sur la médiatrice [AB].
3)Par une méthode algébrique, déterminer l'ensemble E2 des points M tels que z' soit de module 2.
3)(z-zA)/(i(z-zB)=2
Apres remplacement des Z par leur expression et apres reduction, je trouve: x+2y+i(-2x+y+2)=0
Si z' est un réel: x+2y=0, c'est a dire que y=(-1/2)x
Si z' est un imaginaire pur: -2x+y+2=0, c'est à dire que y=2x-2
Donc l'ensemble des solutions est l'intersection entre les deux droites y=(-1/2)x et y=2x-2.
4)Calculer x' et y' en fonction de x et y.
4) D'apres la question precedente j'ai repris les équations des deux droites et j'ai trouver que x=4/5 et y=-2/5.
Mais je ne voi pas comment faire le raprochement avec x' et y'?
5)Par une méthode algébrique, déterminer l'ensemble F des points M tel que z' soit réel. Préciser les ensemble F+ et F- ou z est réel positif ou négatif.
5)D'apres question 3 je sais que ma partie réel est x+2y.
Si z' est réel alors x+2y=0, donc y=(-1/2)x.
donc l'ensemble F+ est ]-l'infini a 0[ et F- est de ]0;+infini[
6)Par une méthode géométrique si possible, déterminer l'ensemble G des points M tels que z' soit imaginaire pur.
6)Je n' ai pas réussi cette question.
7) Prouver que (z'+i)(z-zB) est constant.
Application: si M est sur le cercle de centre B, de rayon 1, ou est M'?
7)je n'arrive pas a prouver que cette une constante.
Verifier et coriger exercice sur complexe
5 messages
- Page 1 sur 1
Bonsoir
3) je ne suis pas d'accord avec la réponse. On doit avoir\mid = 2\mid z+i\mid) car i est de module 1.
car i est de module 1.
En remplaçant z par sa forme algébrique :
\mid =2 \mid x+i(y+1)\mid)
soit en prenant les carrés des modules :
^2+(y+2)^2=4[ x^2+(y+1)^2])
Après réduction, on arrive à

Il faut passer à la forme canonique en divisant d'abord par 3

^2-\frac {4}{9}+(y+\frac {2}{3})^2-\frac {4}{9}-\frac {4}{3}=0)
^2+(y+\frac {2}{3})^2=\frac {20}{9})
On obtient donc un cercle de centre le point de coordonnée) et de rayon
et de rayon 
(Calculs à vérifier , j'ai fait ça rapidement)
4) La question 3 n'est pas utile. Dans l'expression de z', il faut remplacer les complexes par leur forme algébrique et écrire z' sous forme algébrique en multipliant par le conjugué du dénominateur (calculs un peu pénibles)
3) je ne suis pas d'accord avec la réponse. On doit avoir
En remplaçant z par sa forme algébrique :
soit en prenant les carrés des modules :
Après réduction, on arrive à
Il faut passer à la forme canonique en divisant d'abord par 3
On obtient donc un cercle de centre le point de coordonnée
(Calculs à vérifier , j'ai fait ça rapidement)
4) La question 3 n'est pas utile. Dans l'expression de z', il faut remplacer les complexes par leur forme algébrique et écrire z' sous forme algébrique en multipliant par le conjugué du dénominateur (calculs un peu pénibles)
merci bercirj pour ton aide
mais peux tu me dire si la question 1 est juste ou pas, stp
4) Calculer x' et y' en fonction de x et y
z'=(x+iy-2+2i)/(i(x+iy+i)
z'=(x+iy-2+2i) / (ix+i²y+i²)
z'=(x+iy-2+2i) (ix+y-1)/ (ix-y-1) (ix+y-1)
z'=(ix²+xy-x-xy +iy²-iy-2ix-2y+2-2x+2iy-2i) / (-x²+ixy-ix-yix-y²+y-ix-y+1)
mais après comment faire où est le rapport avec x' et y'
5)Par une méthode algébrique, déterminer l'ensemble F des points M tel que z' soit réel. Préciser les ensemble F+ et F- ou z est réel positif ou négatif.
=>comment faire pour préciser les ensembles?
6)Par une méthode géométrique si possible, déterminer l'ensemble G des points M tels que z' soit imaginaire pur.
=>Je bloque sur cette question
7) Prouver que (z'+i)(z-zB) est constant.
=> idem ici, je ne comprend pas vraiment ??
Application: si M est sur le cercle de centre B, de rayon 1, ou est M'?
mais peux tu me dire si la question 1 est juste ou pas, stp
4) Calculer x' et y' en fonction de x et y
z'=(x+iy-2+2i)/(i(x+iy+i)
z'=(x+iy-2+2i) / (ix+i²y+i²)
z'=(x+iy-2+2i) (ix+y-1)/ (ix-y-1) (ix+y-1)
z'=(ix²+xy-x-xy +iy²-iy-2ix-2y+2-2x+2iy-2i) / (-x²+ixy-ix-yix-y²+y-ix-y+1)
mais après comment faire où est le rapport avec x' et y'
5)Par une méthode algébrique, déterminer l'ensemble F des points M tel que z' soit réel. Préciser les ensemble F+ et F- ou z est réel positif ou négatif.
=>comment faire pour préciser les ensembles?
6)Par une méthode géométrique si possible, déterminer l'ensemble G des points M tels que z' soit imaginaire pur.
=>Je bloque sur cette question
7) Prouver que (z'+i)(z-zB) est constant.
=> idem ici, je ne comprend pas vraiment ??
Application: si M est sur le cercle de centre B, de rayon 1, ou est M'?
4. Le dénominateur est -1-y+ix, son conjugué est -1-y-ix (même partie réelle et parties imaginaires opposées). On obtient :
(-1-y-ix)}{(-1-y+ix)(-1-y-ix)}) =
=
^2+x^2}) =
=
}{(-1-y)^2+x^2})
x' est la partie réelle de ce nombre et y' la partie imaginaire ; on a donc :^2+x^2}) et
et ^2+x^2})
5. z' est réel si sa partie imaginaire y' est nulle. Il faut donc que le dénominateur de y' soit non nul et le numérateur nul
Le dénominateur est une somme de 2 carrés , il n'est nul que si y=-1 et x=0 (coordonnées de B)
Pour résoudre - il est plus commode de multiplier par (-1)
il est plus commode de multiplier par (-1)
 . On passe à la forme canonique :
. On passe à la forme canonique : ^2-1+(y+\frac {3}{2})^2-\frac {9}{4}+2=0)
^2+(y+\frac {3}{2})^2=\frac {5}{4})
F est donc le cercle de centre le point de coordonnées
) et de rayon
et de rayon privé du point B
privé du point B
Pour que z' soit un réel positif, il faut que x'>0 soit x+2y+2 >0 soit
On trace la droite (D) d'équation , elle passe par le centre du cercle F donc l'un des 2 demi-cercles obtenus est F+ et l'autre F-. Pour savoir lequel est F+ et lequel est F-, il suffit de prendre un point quelconque du plan par exemple le point O, il vérifie x+2y+2<0 donc le demi-cercle situé du même côté que O par rapport à (D) est F-.
, elle passe par le centre du cercle F donc l'un des 2 demi-cercles obtenus est F+ et l'autre F-. Pour savoir lequel est F+ et lequel est F-, il suffit de prendre un point quelconque du plan par exemple le point O, il vérifie x+2y+2<0 donc le demi-cercle situé du même côté que O par rapport à (D) est F-.
6. EN multipliant numérateur et dénominateur par (-i) . z' est donc imaginaire pur si
. z' est donc imaginaire pur si  c'est-à-dire si il existe un réel k tel que
c'est-à-dire si il existe un réel k tel que  soit
soit  ce qui équivaut à dire que les vecteurs
ce qui équivaut à dire que les vecteurs  sont colinéaires. L'ensemble G est donc la droite (AB) privée du point B.
sont colinéaires. L'ensemble G est donc la droite (AB) privée du point B.
7.}{z-z_B}) donc
donc (z-z_B)=i(z_A-z_B)) constant
constant
En passant aux modules :
Si M appartient au cercle de centre B de rayon 1 alors donc
donc  soit
soit  d'où M' appartient au cercle de centre B de rayon
d'où M' appartient au cercle de centre B de rayon 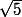
x' est la partie réelle de ce nombre et y' la partie imaginaire ; on a donc :
5. z' est réel si sa partie imaginaire y' est nulle. Il faut donc que le dénominateur de y' soit non nul et le numérateur nul
Le dénominateur est une somme de 2 carrés , il n'est nul que si y=-1 et x=0 (coordonnées de B)
Pour résoudre -
F est donc le cercle de centre le point de coordonnées
Pour que z' soit un réel positif, il faut que x'>0 soit x+2y+2 >0 soit
On trace la droite (D) d'équation
6. EN multipliant numérateur et dénominateur par (-i)
7.
En passant aux modules :
Si M appartient au cercle de centre B de rayon 1 alors
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
