Bonjour à tous,
je bloque sur l'exercice suivant :
il faut chercher si dans Z le produit de trois entiers consécutifs peut être un carré parfait.
Je pense que cela revient à montrer que n^3 + 3*n^2 + 2*n = k^2 où k est un entier. Mais je ne vois pas comment partir.
Merci par avance
Carré parfait
10 messages
- Page 1 sur 1
Salut !
Je te conseille de prendre les entiers consécutifs de cette manière :
n-1, n, n+1
Le produit est)
On veut montrer que c'est un carré parfait.
Il est facile de montrer que n et n²-1 sont premiers entre eux, sauf si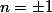 .
.
Ce qui veut dire que si , il faut que n soit un carré parfait et que n²-1 aussi !
, il faut que n soit un carré parfait et que n²-1 aussi !
Or, n² est déjà un carré parfait. Est-ce possible d'avoir deux entiers consécutifs qui sont carrés parfaits ? Ouaip, il n'y a que deux possibilités dans Z :id:
M.
Je te conseille de prendre les entiers consécutifs de cette manière :
n-1, n, n+1
Le produit est
On veut montrer que c'est un carré parfait.
Il est facile de montrer que n et n²-1 sont premiers entre eux, sauf si
Ce qui veut dire que si
Or, n² est déjà un carré parfait. Est-ce possible d'avoir deux entiers consécutifs qui sont carrés parfaits ? Ouaip, il n'y a que deux possibilités dans Z :id:
M.
bjr,.
par exemple, si n est divisible par 7, le multiple suivant
est n+7
n et n+1, n+1 et n+2 sont premiers entre eux.
n et n+2 sont premiers entre eux ou sont tous deux pairs.
1) si n est impair, les trois entiers consécutifs n'ont pas
de facteurs premiers communs deux à deux.
Les trois facteurs sont donc tous les trois des carrés,
or la distance entre deux carrés consécutifs^2) et
et  est 2n+1, qui est rapidement plus grande que 2.
est 2n+1, qui est rapidement plus grande que 2.
par exemple, si n est divisible par 7, le multiple suivant
est n+7
n et n+1, n+1 et n+2 sont premiers entre eux.
n et n+2 sont premiers entre eux ou sont tous deux pairs.
1) si n est impair, les trois entiers consécutifs n'ont pas
de facteurs premiers communs deux à deux.
Les trois facteurs sont donc tous les trois des carrés,
or la distance entre deux carrés consécutifs
re,
voilà la suite,ç'est la même chose.
si n est pair:
n+1 est premier avec n et avec n+2.
n et n+1 n'ont pas de facteurs premiers en commun
n+1 et n+2 n'ont pas de facteurs premiers en commun
n et n+2 sont pairs,
n=2k et n+2=2(k+1)
k et k+1 sont premiers entre eux.
k et 2k+1 sont premiers entre eux.
k+1 et 2k+1 sont premiers entre eux.
Quiite à diviser par 4 le produit n(n+1)(n+2), on est revenu au cas précedent
avec le produit k(2k+1)(k+1) qui doit être un carré et dont les trois facteurs
sont premiers deux à deux.
d'où k,k+1,2k+1 sont tous les trois des carrés parfaits
or (k+1)-k=1, ça laisse peu de possibilités..
voilà la suite,ç'est la même chose.
si n est pair:
n+1 est premier avec n et avec n+2.
n et n+1 n'ont pas de facteurs premiers en commun
n+1 et n+2 n'ont pas de facteurs premiers en commun
n et n+2 sont pairs,
n=2k et n+2=2(k+1)
k et k+1 sont premiers entre eux.
k et 2k+1 sont premiers entre eux.
k+1 et 2k+1 sont premiers entre eux.
Quiite à diviser par 4 le produit n(n+1)(n+2), on est revenu au cas précedent
avec le produit k(2k+1)(k+1) qui doit être un carré et dont les trois facteurs
sont premiers deux à deux.
d'où k,k+1,2k+1 sont tous les trois des carrés parfaits
or (k+1)-k=1, ça laisse peu de possibilités..
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
