Permutations et cycles

[laurie3131]

Bonjour,

Je n'arrive pas à comprendre les permutations et les cycles. Pouvez vous m'aider ?
Je vous donne plusieurs exemples tous indépendants:
soit v = ( 4 5 6 )( 7 8 9)
soit w = ( 1 4 7)( 2 5 8)( 3 6 9)

pourquoi wv= ( 1 4 7)(2 5 8)( 3 6 9)( 4 5 6)( 7 8 9) = ( 1 4 8 3 6 7 2 5 9) ?


Ensuite soit B = ( 1 2 3) et C= ( 1 2 3)
______________( 2 1 3)________( 1 3 2)

pourquoi BoC = ( 1 2 3) ?
_____________( 2 3 1)

Enfin, soit P = ( 1 2 3 4 5 6)
____________( 2 4 6 1 5 3) pourquoi ce n'est pas un cycle ? ( comment sait on si s'en ait un ou pas ? ) Merci pour vos réponses !!

Laurie

[busard_des_roseaux]

Salut,

j'essaye de t'expliquer ,bien que l'algèbre ne soit pas ma tasse de thé:



Les permutations de [|1,n|] forme un groupe pour la composition des applications. Ce groupe a n! éléments, il est donc fini.

C'est le groupe symétrique,noté .

Toute permutation est d'ordre fini,cycles et transpositions comprises.
il y a un moyen simple de décomposer une permutation quelconque
en produit de cycles dont le produit commute, ces cycles
étant à support disjoints.

On considère l'élément 1 et son orbite par , la permutation que l'on souhaite factoriser.

par ex,


Comme tout élément est d'ordre fini, au bout d'un nombre fini d'étapes,
, induit sur ce sous-ensemble
{1,3,4} de [1,n] une permutation de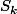 que l'on identifie à un cycle de . On choisit ensuite un élément n'appartenant pas à ce support (içi {1,3,4}) et l'on recommence, ce qui permet d'écrire toute permutation de comme un produit de cycles.


Ensuit(e, il reste à écrire tout cycle comme un produit de transpositions,
pour avoir une famille de générateurs.

[laurie3131]

J'ai rien compris du tout ... :s désolée ...

[busard_des_roseaux]

tu es en quoi ? :doh:

avant de comprendre, il faut apprendre la langue,ie, le vocabulaire:
groupe, sous-groupe, ordre d'un élément, qu'est ce qu'une bijection,une composée de deux applications, un cycle, une transposition. Ce n'est pas sorcier.

[laurie3131]

L1 maths info et je suis en ratrapage la semaine prochaine. tu ne peux pas m'expliquer sur mes exemples s'il te plait ?
Et oui, pour moi c'est sorcier ...

[busard_des_roseaux]

soit v = ( 4 5 6 )( 7 8 9)
soit w = ( 1 4 7)( 2 5 8)( 3 6 9)

Les éléments considérés vont de 1,2...jusqu'à 9.
On considère que v et w appartiennent à


Comme je te l'ai raconté, toute permutation peut s'écrire en produit de cycles , de support disjoint.

wv signifie la composée de v suivie de w (la composition des applications s'écrit de droite à gauche)

On regarde l'image de 1 par wv.
d'abord v.
v laisse invariant 1 , v(1)=1, car 1 n'appartient pas au support de v.
d'où
wv(1)=w(1)=4
le premier cycle de wv commence donc par:
(14
on cherche l'image de 4 par wv:
v(4)=5 , wv(4)=w(5)=8
le premier cycle de wv commence donc par:
(148

et le procédé continue jusqu'à retrouver 1.
Ce qui donnera le 1er cycle de wv.
Et en fait wv est un cycle,de longueur 9.

[laurie3131]

Merci vraiment bcp ! j'ai compris comment ca fonctionnait maintenant :)

[laurie3131]

Et pour les cycles, comment sait ton si s'en est un ou pas ? ( par exemple P que j'ai énoncé plus haut )

[busard_des_roseaux]

Enfin, soit P = ( 1 2 3 4 5 6)
____________( 2 4 6 1 5 3) pourquoi ce n'est pas un cycle ? ( comment sait on si s'en ait un ou pas ? )

Cette dernière notation est une "vieille" notation, qui n'a rien à voir avec l'écriture "moderne" d'une permutation en produit de cycles.
Il importe donc de la traduire dès le début.
Dans cette notation, l'image de 1, est notée sous 1,
et non pas à sa suite.

[laurie3131]

Merci encore. :we: