Suite Question pas si facile pour moi :-D

[mathmath06]

Bonjour j'ai un exercice sur les suites et je me pose une question l énoncé me di que lim lU(n)l=2 quand n->+l'infini et U(n+1)-Un<1 Pour tout n de N
Montrer qu'a partir d'un certain rang U(n) appartient ]-3;-1[U]1;3[

Merci d'avance pour l'aide

[masiuxus]

Je suppose avant tout que c'est |u(n+1)-u(n)|<1 ...
Cela dit, je ne vois pas trop l'intérêt de cette condition.

Si u(n) tend vers 2 à l'infini, alors il existe un rang N à partir duquel :
| |u(n)| - 2| < 1. Ceci équivaut à dire que :

-1 < |u(n)| - 2 < 1

donc à :

1 < |u(n)| < 3. CQFD.

[mathmath06]

merci sa m'a aidé a repondre a cette question mais la suivante aussi me cause probleme il faut en deduire que la suite U(n) garde un signe constant a partir d un certain rang (indice : possibilité de raisonner par l'absurde) et ch'ui toujours en galere pour le trouver :-s

[masiuxus]

Et bien suis la consigne : suppose qu'à partir d'un certain rang, les termes successifs ne sont pas de signe constant ... est-ce que ça ne rentre pas en contradiction avec ce que l'on a démontré à la question précédente ?

[magnolia86]

A la place d'une preuve par l'absurde, je ferai une récurrence rapide et simple.

Les hypothèses précisent ceci :
pour tout supérieur à certain rang , on a et .

Ainsi donc .
* Si alors .
Or donc , comme .
* Si alors .
Or donc , comme .

Dans tous les cas et appartiennent au même intervalle, et cela pour tout . D'où le résultat...


Cela dit, parfois les indications sont des ordres déguisés...

Edit : j'attends de voir la preuve par l'absurde car elle me paraît un peu compliquée pour un niveau lycée.

[mathmath06]

merci je me sens stupide des fois ^^

[magnolia86]

Ah mais tu ne vas pas t'en tirer comme ça ! :ptdr:
Fais-nous une preuve par l'absurde puisque ton énoncé le conseille.

[mathmath06]

oula ben ok je vais essayé (soit disant c'est dur pour un niveau lycée merci c'est gentil de me le faire faire ... :p

[magnolia86]

Bon, je laisse la preuve par l'absurde qui me vient à l'esprit. Peut-être que quelqu'un aura quelque chose de plus simple ! Ce serait bien !

C'est le début qui me parait difficile à trouver pour un lycéen, même en TS je crois...

Les hypothèses précisent ceci :
pour tout , on a , et donc .

Ainsi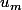 n'est pas de même signe que , mais, par minimalité de , le terme est de même signe que , donc et n'ont pas le même signe. Or ces deux termes appartiennent à , et donc puisqu'ils n'ont pas les mêmes signes. Or cela contredit l'hypothèse .

Conclusion : la suite est de signe constant à partir de !


Qu'en penses-tu ?

[lapras]

salut,
c'est un peu faire de l'absurde pour faire de l'absurde mais bon ! (heureusement que léon n'est pas la pour voir ton post). En tout cas tu mets en valeur le principe de l'extremum c'est sympa pour un TS.

[magnolia86]

salut,
c'est un peu faire de l'absurde pour faire de l'absurde mais bon ! (heureusement que léon n'est pas la pour voir ton post). En tout cas tu mets en valeur le principe de l'extremum c'est sympa pour un TS.

Léon :look2: le tueur à gage de Luc Besson ? :look:

Je suis d'accord avec toi : ici, c'est passablement compliqué de faire un raisonnement par l'absurde. Mais ce qui est étonnant, c'est qu'il s'agit de l'indication donnée par l'énoncé de mathmath06...

[mathmath06]

et que je passe seulement en terminale :mur:

[magnolia86]

et que je passe seulement en terminale :mur:

:doh: Et tu as compris la preuve par l'absurde ?

[Dominique Lefebvre]

RAPPEL AU REGLEMENT :

Je vous rappelle qu'il n'est pas dans la politique du forum que de donner les solutions... Certains ont l'air de l'oublier! La prochaine fois, je ne modifie plus les messages (c'est lassant), je supprime la discussion. En cas de récidive, je vire le coupable!

[magnolia86]

(...)Certains ont l'air de l'oublier! (...)

"Certains", "on", c'est trop vague : vous ne pouvez pas appeler les forumeurs par leur pseudo ? Ce serait plus clair.
Et avec un petit message en MP pour marquer le carton jaune, ça éviterait de désagréables surprises.

Cela étant dit, ici, je ne vois pas comment un élève passant en TS peut raisonnablement réaliser cette preuve par l'absurde correctement (c'était pourtant conseillé par l'énoncé). Autant lui montrer à quoi ça doit ressembler. Mais si on reste vague, les choses sont trop souvent comprises de travers...

[Clembou]

"Certains", "on", c'est trop vague : vous ne pouvez pas appeler les forumeurs par leur pseudo ? Ce serait plus clair.
Et avec un petit message en MP pour marquer le carton jaune, ça éviterait de désagréables surprises.

Cela étant dit, ici, je ne vois pas comment un élève passant en TS peut raisonnablement réaliser cette preuve par l'absurde correctement (c'était pourtant conseillé par l'énoncé). Autant lui montrer à quoi ça doit ressembler. Mais si on reste vague, les choses sont trop souvent comprises de travers...

Non ! Non ! "Certains ont l'air de l'oublier" est bien orthographié. C'est vrai que là, tu (oui, le message de Dominique s'adressait à toi) viens de donner le raisonnement que devait trouver notre cher ami. :--: Dommage que tu ne respectes pas les régles du forum :triste:

[magnolia86]

Non ! Non ! "Certains ont l'air de l'oublier" est bien orthographié.

Je sais, merci :zen:

C'est vrai que là, tu (oui, le message de Dominique s'adressait à toi) viens de donner le raisonnement que devait trouver notre cher ami. :--: Dommage que tu ne respectes pas les régles du forum :triste:

Crois-tu qu'il était capable de la faire ? Je reprécise qu'il passe en terminale... En plus, on ne sait même pas s'il a compris celle que je lui ai donnée. J'aurais bien voulu savoir. Dommage.

[Clembou]

Je sais, merci :zen:



Crois-tu qu'il était capable de la faire ? Je reprécise qu'il passe en terminale... En plus, on ne sait même pas s'il a compris celle que je lui ai donnée. J'aurais bien voulu savoir. Dommage.

Voilà ! Tu le dis par toi-même... Vaut mieux un raisonnement point par point par des questions claires et précises (cf : http://maths-forum.com/showthread.php?t=67095) que de balancer ton raisonnement que notre ami comprendra une fois sur ... (à toi d'en juger).

Désolé, mon message peut paraitre agressif mais un rappel d'un point fondamental du réglement du forum était nécessaire pour éviter ce genre de dérives.

[magnolia86]

Voilà ! Tu le dis par toi-même... Vaut mieux un raisonnement point par point par des questions claires et précises (cf : http://maths-forum.com/showthread.php?t=67095) que de balancer ton raisonnement que notre ami comprendra une fois sur ... (à toi d'en juger).

ok, j'aurais pu couper la démo en deux, à la moitié du raisonnement, et demander de terminer...

Mais que pensez-vous de la toute première réponse de masiuxus ? N'incite-t-il pas le pauvre lycéen à faire comme si la limite de existait ? Je serais bien curieux de savoir comment mathmath06 à rédiger sa réponse...

Désolé, mon message peut paraitre agressif mais un rappel d'un point fondamental du réglement du forum était nécessaire pour éviter ce genre de dérives.

J'espère que ce genre de rappel est/sera systématique (car de nombreux messages contiennent des preuves entières, surtout quand elles sont courtes), et non en fonction de l'humeur de "certains".

So, wait and see.

[Clembou]

ok, j'aurais pu couper la démo en deux, à la moitié du raisonnement, et demander de terminer...


J'espère que ce genre de rappel est/sera systématique (car de nombreux messages contiennent des preuves entières, surtout quand elles sont courtes), et non en fonction de l'humeur de "certains". Par exemple, que pensez-vous de la toute première réponse de masiuxus ? C'est bon, il peut le faire lui ?... (en plus, il insite le pauvre lycéen à faire comme si la limite de existait !)

So, wait and see.

Même de la couper en n parties, cela ne se fait pas ! Désolé :triste: ! Masiuxus est aussi "en infraction" (je ne l'avais pas vu, tu m'en excuseras :id: ). Essayez de faire comme j'ai fait dans le post que je vous ai donné. Je poses les questions justes, je ne donne en aucun cas LA réponse toute faite.

Le tout est de s'assurer que notre ami (c'est comme cela que j'appelle celui qui poste) a bien compris ce qu'il lui a été demandé. Je vous le rappelle une fois mais après c'est le modérateur qui vous avertira.