2)Trouver toutes les fonctions f telles que :
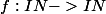
 \in IN^2, f(m^2 + n^2) = f(m)^2 + f(n)^2)
Jolie solution, tu as trouvé la bonne factorisation
on peut utiliser ce lemme de fermat :
p premier tel que p=1[4] il existe a et b entiers naturels tels que p = a² + b²
puis on peut utiliser l'égalité
(a²+b²)(c²+d²) = (ac+bd)² + (ad - bc)²
ce qui montre
que tout entier congru a 1 mod 4 peut etre calculé grace a cette identité remarquable
ce qui nous fait penser aux restes dans la division par 4 et nous fait donc chercher l'égalité :
(4q+r)² = (4q-r)² + (2q+2r)² - (2q-2r)²
par récurrence forte, f(n) = n :happy2:
autre solution :
tout nombre entier naturel peut s'écrire sous la forme de 5x+2y
avec x et y entiers
preuve :
théoreme de bezout :
il existe (u ; v) dans Z² tels que 5u + 2v = 1
=>
n = 5*(un) + 2*(vn)
x = u*n
y = v*n
ce lemme démontrer, on peut "remarquer que" :
(5x+2y)² + y² = (4y + x)²+ (3y + 2x)²
par récurrence forte, on fini par démontrer que f(n) = n
cqfd
