Limite d'une fonction non majorée

[chipie01]

Bonjour,
On sait que f est une fonction continue, dérivable sur R et que sa dérivée est positive. D'autre part on a :
quel que soit t appartenant à R, f(t+2Pi)=f(t)+2Pi
On veut montrer qu'alord limite de f(t) en plus l'infini est plus l'infini.

Je vous remercie d'avance pour votre aide.

[Alpha]

Salut,

A première vue, on peut essayer de montrer que f n'est pas majorée. Comme de plus sa dérivée est positive, elle est croissante, et une fonction croissante et non majorée tend vers + l'infini.

Reste donc à montrer que f n'est pas majorée, ce qui est trivial (c'est là qu'on utilise f(t + 2pi) = f(t) + 2pi ). Je te laisse chercher un peu, si tu ne trouves pas, dis-le, et je détaillerai ce dernier point.

Alpha +

[chipie01]

Oui c'est justement le point de la majoration qui m'empêchait de démontrer que limite en plus l'infini est égale a plus l'infini.
Merci pour ton aide

[Alpha]

Salut,

Soit un réel. Soit un réel quelconque.

Si , ne majore pas .

Sinon, on a donc . Et il existe
tel que .

Pour le montrer rigoureusement, il suffit de dire que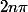 tend vers + l'infini quand tend vers + l'inf, donc il existe tel que .

Or , donc .

Donc, quel que soit le réel , ne majore pas . n'est donc pas majorée.

CQFD.

Alpha +

[chipie01]

Merci bcp alpha et je ferai attention de bien respecter les consignes du forum désormais.
Chipie ;-)