Suite réelle non majorée

[jonses]

Bonjour ou bonsoir,

Je n'arrive pas à monter que :

si est suite réelle non majorée, alors il existe une suite extraite de qui tend vers


Si quelqu"un peut m'aider je le remercie d'avance.

[eratos]

Bonjour ou bonsoir,

Je n'arrive pas à monter que :

si est suite réelle non majorée, alors il existe une suite extraite de qui tend vers


Si quelqu"un peut m'aider je le remercie d'avance.

Salut!
u n'est pas majorée donc tend vers infnty... tu prends u pour suite extraite?

[jonses]

Salut!
u n'est pas majorée donc tend vers infnty... tu prends u pour suite extraite?

C'est pas plutôt u n'est pas majorée et croissante, donc elle tend vers ?

[eratos]

C'est pas plutôt u n'est pas majorée et croissante, donc elle tend vers ?

oui :lol3:

[Ben314]

Dire que "la suite est majorée" signifie que :
"Il existe un réel M tel que, pour tout entier n, on a "

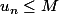
Donc, dire que "la suite n'est pas majorée" signifie que :
.....

et, à l'aide de cette proposition, il faut que tu trouve une fonction strictement croissante telle que, (par exemple...), pour tout n.
Cela prouvera que la suite extraite tend vers l'infini.

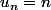
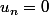
P.S. Une suite non majorée ne tend pas forçément vers l'infini, par exemple, si pour n pair et pour n impair, la suite n'est pas majorée, mais ne tend pas vers l'infini non plus (par contre la suite extraite qui ne contient plus que les termes d'indice pair tend vers l'infini)

[eratos]

oui pardon. :lol3:

Donc ce que tu peux faire:

tu construis une sous suite ....
avec >i (i de 1 à k) ce qui est possible avec les hypothèses.

quand k -> oo on a ->oo

[jonses]

Dire que "la suite n'est pas majorée" signifie que :
"Pour tout réel M, on dispose d'un entier p, tel que "

C'est la recherche d'une fonction strictement croissante qui me pose beaucoup de difficultés.
J'ai essayé de m'inspirer du lemme des pics pour tenter de construire une suite extraite croissante, mais en vain

[Ben314]

Vu que
"Pour tout réel M, on dispose d'un entier p, tel que "

En prenant M=1, cela montre qu'il existe un entier tel que
En prenant M=2, cela montre qu'il existe un entier tel que
etc...
Mais, il y a effectivement un "problème technique" : est on sûr que (puis que , etc...)
A priori, non, on en est pas sûr vu ce qu'on a écrit pour le moment.

Il y a (au moins) deux façon de remédier au problème :

- Soit montrer qu'il existe un entier strictement plus grand que tel que (pas trés difficile, par exemple en raisonnant par l'absurde)
- Soit (un peu plus joli) dire que pour on a pris le plus petit entier tel que puis que, pour on a pris le plus petit entier tel que ce qui assure que