Démontrer que log est continue sur ]0;+inf[

[aze321]

Bonjour,

Comment démontrer que la fonction est continue sur ?

Pouvez vous m'aider, svp!

[Nightmare]

Bonsoir,

il suffit de montrer qu'elle y est dérivable en revenant à la définition avec les taux d'accroissements.

[aze321]

Bonsoir Nightmare,

J'ai essaiyé de le démontrer avec le test de continuité suivant:
f(x)=log(x) est continue en 0 si :





Et comme log(0) n'est pas une valeur réelle on sait que cette fonction n'est pas continue en x=0 mais comment faire pour montrer quelle est continue sur l'intervalle

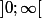
je vais voir avec t(h)...

[aze321]

la fonction f(x)=log(x) n'étant pas continue en 0 elle n'est donc pas non plus dérivable en 0 comme le montre le test du taux d'accroisement suivant:


=indéterminé comme on pouvait s'y attendre
on voit que log(x) admet une tangente vericale en x=0+
mais comment on en arrive à démontrer la continuité?
Merci pour ton aide!

[aze321]

quelqu'un peut m'aider, svp?
jp

[uztop]

Salut,

quelle est la définition de la fonction log ? Elle est généralement définie comme étant la fonction dont la dérivée est 1/x.
A partir de là, tu peux montrer qu'elle est dérivable sur R+* et qu'elle y est donc continue

[aze321]

ok juste pour info comment on montrer que 1/x est dérivable et donc continue sur R+*
merci,
jp

[Huppasacee]

Pour x différent de 0, calcule

limite quand h tend vers 0 de :

[1/(x=h) - 1/x] /h

en mettant au même dénominateur etc;..

[Huppasacee]

ln (a + h )= lna + ln (1 + h/a)

Pour démontrer que ln est continue pour tout x strictement positif, il suffit de démontrer qu'elle est continue en 1

Utiliser alors la définition

lnx = intégrale de 1 à x de 1/t dt

encadrer 1/t et conclure