Merci beaucoup pour tout !!!
J'vais essayer de finir l'exo tout seul quand même ;-)
Et au passage, c'est pas ASTROX, mais AsTr0x (avec un zéro ^^)
[Term] Suite et récurrence (Grand Merci en particulier à La
33 messages
- Page 2 sur 2 - 1, 2
C'est bien parceque tu m'a aidé que j'te pardonne ^^
Plus sérieusement, je comprend pas trop pourquoi tu m'avais dis que la démonstration que (Un) est décroissante ne suffisait pas...
j'avais fait :
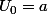
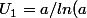)
comme :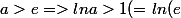))
donc U_1)
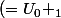)
Ainsi comme P(n) ==> P(n+1), Ceci peut se généraliser à Un > U(n+1)
Si tu peut me dire brièvement comment faire, car pour moi ça suffirait ^^
Plus sérieusement, je comprend pas trop pourquoi tu m'avais dis que la démonstration que (Un) est décroissante ne suffisait pas...
j'avais fait :
comme :
donc
Ainsi comme P(n) ==> P(n+1), Ceci peut se généraliser à Un > U(n+1)
Si tu peut me dire brièvement comment faire, car pour moi ça suffirait ^^
Mais étant donné que l'hérédité a été prouver, on a U(n) > e, si on cherche juste à démontrer que la suite est décroissante (ou croissante, si je me trompe), quelle démarche faudrait-il adopter ?
Si je cherche, c'est pour ma culture, pour savoir comment faire si j'ai ce genre de question au BAC, car j'ai feuilleter le livre, et ce genre de question tombe assez souvent (démontrer que la suite est croissante/décroissante)
Si je cherche, c'est pour ma culture, pour savoir comment faire si j'ai ce genre de question au BAC, car j'ai feuilleter le livre, et ce genre de question tombe assez souvent (démontrer que la suite est croissante/décroissante)
donc bon j'ai fait le calcul dans le message précédent :
et je trouve :
U(n) - f(Un) > 0 (= [Un*ln(Un) - Un] / [ln(Un)] avec ln(un) > o car u(n) > e )
f(Un) - U(n) < 0
j'vais épargné le reste, le principal c'est que j'ai compris ^^
si je me suis pas trompé ?
et je comprend mieux que dans les 2 sens c'est pareil ;-)
Encore merci pour tout !
Et puis peux etre à bientot ^^
et je trouve :
U(n) - f(Un) > 0 (= [Un*ln(Un) - Un] / [ln(Un)] avec ln(un) > o car u(n) > e )
f(Un) - U(n) < 0
j'vais épargné le reste, le principal c'est que j'ai compris ^^
si je me suis pas trompé ?
et je comprend mieux que dans les 2 sens c'est pareil ;-)
Encore merci pour tout !
Et puis peux etre à bientot ^^
33 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 105 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
