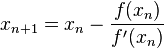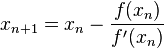Methode de Newton

[zelda007]

Bonjour,

Sur de nombreux sites, j'ai vu que la formule de réccurence pour trouver les zeros d'une fonction est :


Pourtant, je me demande si cette formule est facilement démontrable avec une reccurence par exemple ?

Merci :we:

[ThSQ]

Commence par faire un dessin pour voir comment ça évolue (tangente tout ça ...).

[zelda007]

Je sais très bien comment ca marche graphiquement (j'ai le graphe devant moi) mais je me demandais si il etait possible de démontrer cette formule par le calcul ou une récurrence (et pas graphiquement) ?

Merci

[Memento]

Bonsoir,

Tu imagine par exemple une courbe croissante sur R+ et qui coupe l'axe des Ox.

Si tu considère le point ou la courbe de f coupe l'axe des abscisses.

Tu pars de situé a droite de et tu considère alors la tangente en a la courbe de f.
Cette tangente de pente coupe l'axe des abscisses en (situé entre et sur l'axe des abscisses, on se rapproche donc de vers la gauche.

A partir de , on s'est donc déplacé de vers la gauche, et on a donc:



Tu verifie graphiquement que :

(la pente de la tangente secante avec Ox en )


D'ou:

Et enfin


@+

[zelda007]

C'est plus une démo graphique mais bon :)

Sinon, j'ai pas bien compris l'histoire du "b" et je n'arrive pas à le placer sur mon graphe. Tu pourrais me donner un exemple avec la fonction Sqrt(x) par exemple ?

Merci

[BQss]

Le théorème sous jacent c'est un théorème de point fixe.

Si non, l'idée est de minimiser la fonctionnelle |f(x)-f(x0)|(on prend x0 =0 pour chercher le zéro ici par exemple), tu calcules a chaque xn la dérivée |f(xn)|' qui est f'(xn) quand f(xn)>0 et -f'(xn) si non, et tu sais que la direction de minimisation d'une fonction positive, c'est l'opposée de la dérivée(voir méthode de gradient en dimension superieur), c'est a dire que quand ca decroit on avance et quand ca croit on recule.

donc on va chercher un xn+1=xn+signe_opposé_de(|f(x)|')*Kn avec Kn une constante qui peut dépendre de n et qui est le pas.

dans la méthode de newton on vérifie qu'on a deja bien quand f(xn)>0, |f(xn)|'=f'(xn) et donc il faut avancer dans le sens -f'(xn) ce qui est le cas lorsque l'on fait xn+1=xn-f(xn)/f'(xn).
Pareil quand f(xn) est negatif, la dérivée de la valeur absolue vaut -f'(xn) et on doit donc avancer dans le sens f'(xn), et comme -f(xn)>0 c'est a nouveau ce qu'on fait en faisant xn+1=xn-f(xn)/f'(xn).


Conclusion, mathématiquement si la fonction est dérivable ailleurs qu'en 0, tu avances bien vers le zero.

Ensuite, cet algorithme n'est pas stable numériquement dans tout les cas.
Et pour ce qui est du pas kn de la méthode de newton, il s'explique par le fait que plus la dérivée est petite, plus il va valloir avancer car on se rapprochera moins vite du zero, alors que plus elle est grande moins il faudra se rapprocher, ce qui justifie la dérivée au denominateur.

Pour ce qui est du f(xn) au numerateur, meme genre, plus tu es loins de 0 plus il faudra avancer et plus tu es pres moins il faudra avancer...

Donc ca c'est les 3 raisons pratiques, ensuite vient s'ajouter a ca la preuve de la convergence, qui est donc une consequence de théorème de point fixe, tu trouveras dans des bouquins et sur le net, et tu y trouveras aussi la vitesse de convergence.

PS:Ce qu'il faut bien comprendre c'est que c'est comme ca qu'on procede, on cherche une methode numerique intelligente(dérivée en dessous, valeur au dessus, direction opposée a la variation) et ensuite on valide en donnant les caracteristiques et les eventuels problemes(dans cette methode le problème de stabilité intervient quand la dérivée est beaucoup trop grande), et avant cette preuve de convergence, on a deja la preuve qu'on se redirige au moins vers le zero, meme si on peut le dépasser de trop...

[Memento]

Pour b :

Tu pars de sur l'axe des abscisse et tu te déplace vers la gauche de jusqu'a point ou la tangente en à la courbe de coupe l'axe .

Tu as donc la pente de la tangente

@ +

[zelda007]

Merci à vous :)