Bonsoir a vous
Soit (an) la suite definie par la relation de recurrence
A0 = 1
An+1 = An + 2A(n-1) + 3A(n-2) + ... + (n+1) A0
il faut calculer la fonction génératrice A(x) = Somme (An * x^n) pour n>=0
Pour le calcul de la fonction génératrice d'habitude je ne rencontre pas de probleme particulier, mais An est donné sous la forme An = ...
Ma question est comment transforme t on An+1 en An?
Merci pour vos reponses
Fonction generatrice, calcule de la suite
8 messages
- Page 1 sur 1
Bonjour,
on doit avoir une forme explicite de , si tu calcules les premiers termes tu peux remarquer qu'il s'agit d'un terme sur deux dans la suite de Fibonacci : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ... (à démontrer...)
, si tu calcules les premiers termes tu peux remarquer qu'il s'agit d'un terme sur deux dans la suite de Fibonacci : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ... (à démontrer...)
La suite de Fibonacci pouvant s'écrire :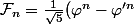) avec
avec 
on doit avoir une forme explicite de
La suite de Fibonacci pouvant s'écrire :
Merci pour votre reponse, il faut donc que je calcule les premiers termes de la suite pour trouver une ressemblance...
Donc par exemple, pour celui ci:
An+1 = An + A(n-1) + ... + A0
A0 = 1
Les premiers termes sont
1, 1, 2, 4, 8
Donc A(n+1) = 2*An ainsi An = 2^n*A0
Est-ce cela?
Pour revenir a l'exemple de mon premier message, la suite An s'exprime de quelle facon, j'avoue ne pas savoir.
Donc par exemple, pour celui ci:
An+1 = An + A(n-1) + ... + A0
A0 = 1
Les premiers termes sont
1, 1, 2, 4, 8
Donc A(n+1) = 2*An ainsi An = 2^n*A0
Est-ce cela?
Pour revenir a l'exemple de mon premier message, la suite An s'exprime de quelle facon, j'avoue ne pas savoir.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
