DM de MATHS en terminale ES
27 messages
- Page 1 sur 2 - 1, 2
DM de MATHS en terminale ES
Salut à tous. Alors voilà je suis en terminale ES, j'ai un DM de math à faire il y a trois exercices j'ai réussi à en faire un mais les deux autres je bloque.
Alors voici tout d'avord l'énoncé du premier.
Exercice 1
f est la fonction définie sur R\{3}
f(x) = ax + b + 1/3-x où a et b sont des réels.
On note C la représentation graphique de f dans un repère .
1. Déterminer a et b pour que la courbe C passe pas le point A ( 2;1 ) et admette en ce point une tangente horizontale.
2.a) Demontrer que la droite delta d'équation y= -x + 2 est asymptote a C.
b) Etudier la position relative de la courbe C par rapport a delta.
3. Etudier la limite de f en 3.
4. etudier les variations de f.
5. représentez C.
Pourriez vous vraiment m'aidez surtout pour le début, car déjà en math je n'ai pas un bon niveau et là avec ce devoir je passe tout mon temps dessus et j'aimerai qu'avec votre aide je puisse le finir rapidement.
Si pour une aide plus rapide vous voulez mon msn envoyer moi un message privé merci.
Alors voici tout d'avord l'énoncé du premier.
Exercice 1
f est la fonction définie sur R\{3}
f(x) = ax + b + 1/3-x où a et b sont des réels.
On note C la représentation graphique de f dans un repère .
1. Déterminer a et b pour que la courbe C passe pas le point A ( 2;1 ) et admette en ce point une tangente horizontale.
2.a) Demontrer que la droite delta d'équation y= -x + 2 est asymptote a C.
b) Etudier la position relative de la courbe C par rapport a delta.
3. Etudier la limite de f en 3.
4. etudier les variations de f.
5. représentez C.
Pourriez vous vraiment m'aidez surtout pour le début, car déjà en math je n'ai pas un bon niveau et là avec ce devoir je passe tout mon temps dessus et j'aimerai qu'avec votre aide je puisse le finir rapidement.
Si pour une aide plus rapide vous voulez mon msn envoyer moi un message privé merci.
Si le point (2;1) est sur la courbe, ses coordonnées vérifient l'équation de la courbe -> une équation.
Si la tangente au point (2;1) est horizontale, que vaut son coefficient directeur ? Que peut-on en déduire sur f'(2) ? -> deuxième équation.
Et v'là, deux équations, deux inconnues, ça roule :)
Si la tangente au point (2;1) est horizontale, que vaut son coefficient directeur ? Que peut-on en déduire sur f'(2) ? -> deuxième équation.
Et v'là, deux équations, deux inconnues, ça roule :)
« Je ne suis pas un numéro, je suis un homme libre ! »
Si le point ( x_A ; y_A ) est sur la courbe, on a 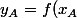 = a \times x_A + b + \frac{1}{3-x})
Ici, tu prends et
et 
Ensuite, le coefficient directeur est bien 0.
Et tu sais que le nombre dérivé représente le coefficient directeur de la tangente au point considéré.
Donc tu as f '(2) = 0
Il faut donc que tu calcules f ' .
Bon courage
Ici, tu prends
Ensuite, le coefficient directeur est bien 0.
Et tu sais que le nombre dérivé représente le coefficient directeur de la tangente au point considéré.
Donc tu as f '(2) = 0
Il faut donc que tu calcules f ' .
Bon courage
« Je ne suis pas un numéro, je suis un homme libre ! »
Qu'est ce que tu ne comprends pas ?
La droite est asymptote à la courbe si la courbe se rapproche de plus en plus de la droite, donc que la distance entre la droite et la courbe se rapproche indéfiniment de 0.
Donc la différence entre les 2 équations tend vers 0.
La droite est asymptote à la courbe si la courbe se rapproche de plus en plus de la droite, donc que la distance entre la droite et la courbe se rapproche indéfiniment de 0.
Donc la différence entre les 2 équations tend vers 0.
« Je ne suis pas un numéro, je suis un homme libre ! »
C'est ça !
Donc la droite est asymptote à la courbe.
Pour avoir la position relative, tu dois chercher le signe de f(x) - (-x+2).
Si c'est positif, la courbe de f est au dessus de la droite, si c'est négatif, la droite est au dessus de la courbe.
Donc la droite est asymptote à la courbe.
Pour avoir la position relative, tu dois chercher le signe de f(x) - (-x+2).
Si c'est positif, la courbe de f est au dessus de la droite, si c'est négatif, la droite est au dessus de la courbe.
« Je ne suis pas un numéro, je suis un homme libre ! »
27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
