Probleme d'Algèbre intouchable.
21 messages
- Page 1 sur 2 - 1, 2
Probleme d'Algèbre intouchable.
Bonjour,
J'ai un petit soucis sur un probleme d'Algèbre.
Enoncé:
Soit E un R-ev. on note Id l'applicat° identité de E et o l'applicat° nulle. Si f est endomorphisme de E on note f°=Id et f^n=f o f^n-1 pout tout entier n>1. Soit a et b 2 R/{0}. On désigne par P l'applicat° de L(E) ds L(E) défnie par P(f)= f² + af + b Id pour tout endomorphisme f de E.
1) P est-elle une application linéaire?
2) Montrer que si le trinome x²+ax+b admet une racine réelle, alors il existe au moins un endo f de E tel que P(f)=0.
3) soit f elts de E tel que P(f)=0.
a) Montrer que si b différent de 0, f est bijective et déterminer son inverse en fction de f.
b) peut on avoir f bijective et b=0.
SVP aidez moi j'en peu plus c un véritable casse tête.
J'ai un petit soucis sur un probleme d'Algèbre.
Enoncé:
Soit E un R-ev. on note Id l'applicat° identité de E et o l'applicat° nulle. Si f est endomorphisme de E on note f°=Id et f^n=f o f^n-1 pout tout entier n>1. Soit a et b 2 R/{0}. On désigne par P l'applicat° de L(E) ds L(E) défnie par P(f)= f² + af + b Id pour tout endomorphisme f de E.
1) P est-elle une application linéaire?
2) Montrer que si le trinome x²+ax+b admet une racine réelle, alors il existe au moins un endo f de E tel que P(f)=0.
3) soit f elts de E tel que P(f)=0.
a) Montrer que si b différent de 0, f est bijective et déterminer son inverse en fction de f.
b) peut on avoir f bijective et b=0.
SVP aidez moi j'en peu plus c un véritable casse tête.
re
Salut à tous,
pour la 2, soit la racine réelle de x²+ax+b. Alors considérons f l'homothétie de rapport
la racine réelle de x²+ax+b. Alors considérons f l'homothétie de rapport 
pour tout x,
P(f)(x) = f²(x)+af(x)+b.x=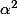 x +a
x +a x + bx
x + bx
=(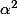 + a
+ a  +b ) x = 0.x = 0
+b ) x = 0.x = 0
d'ou p(f) est l'application nulle
pour la 2, soit
pour tout x,
P(f)(x) = f²(x)+af(x)+b.x=
=(
d'ou p(f) est l'application nulle
re
Pour la 3a), il suffit de trouver g tel que f.g = Id, ce qui doit être facilement faisable en faisant passer b Id du côté du 0 et en divisant par b ...
mounem a écrit:pour la question 3b)
je dirais que P(f)=f²+af= f (1+af)=0 f=0 ou f=1/ (-a) et après comment conclure sur la bijection.
avant d'écrire quelque chose, demande toi à quel ensemble appartient l'élément, quel est cet ensemble (groupe, anneau, espace vectoriel ...) et par conséquent qu'aie-je le droit de faire avec mon élément ?
Si tu suis ces conseils, tu devrais pouvoir t'en sortir en algèbre pendant toute la prépa.
Ici, tu as écrit n'importe quoi, écris des choses qui ont du sens, et tu trouveras la solution.
kazeriahm a écrit:salut
pour la 1) P(f) est clairement linéaire (f^2 c'est pas f*f qui n'a pas de sens mais bien f ° f, la composée de f par f, qui est encore linéaire) comme somme d'applis linéaires (L(E) est un ev)
oula, autant se gourrer en etant aussi peremptoire c'est du joli
ici fof=f*f vu que f est une application lineaire elle meme(meme si on a meme pas besoin de le voir comme ca pour repondre), d'ailleurs tu aurais pu voir que tout le monde l'avait signalé, ca t'aurait évité de raconter n'importe quoi
c'est donc CLAIREMENT non lineaire vu que afo(af)=a^2fo(f) qui est different de afof ( ce qui implique que aP(f) differe de P(af) ), meme pas besoin d'ecrire f^2(f^2 est d'ailleurs une notation pour fof donnée dans l'énoncée et qui se comprend tres bien dans le cas ou f est une appli lineaire...), juste de remarquer que l'on peut ressortir le a du fait de la linearité de f...
a plus et bonne année
PS: la prochainefois fois lis les autres. Et jette un coup d'oeil a l'application d'un peu plus pres elle est defini sur les endomorphisme de E...
BQss a écrit:oula, autant se gourrer en etant aussi peremptoire c'est du joli!
ici fof=f*f vu que f est une application lineaire elle meme(meme si on a meme pas besoin de le voir comme ca pour repondre), d'ailleurs tu aurais pu voir que tout le monde l'avait signalé, ca t'aurait évité de raconter n'importe quoi. Par ailleurs ta justification est fausse, sans compter que f*f a bien un sens qui est certes en effet different de fof en general, sauf que ici c'est vrai pas de chance :zen: . Je crois que tu t'es melangé les pinceaux entre f qui est une appli lineaire et l'appli P défini sur L(E) qui elle ne l'est pas.
c'est donc CLAIREMENT non lineaire vu que afo(af)=a^2fo(f) qui est different de afof ( ce qui implique que aP(f) differe de P(af) ), meme pas besoin d'ecrire f^2(f^2 est d'ailleurs une notation pour fof donnée dans l'énoncée et qui se comprend tres bien dans le cas ou f est une appli lineaire...), juste de remarquer que l'on peut ressortir le a du fait de la linearité de f...
a plus et bonne année.
PS: la prochainefois fois lis les autres. Et jette un coup d'oeil a l'application d'un peu plus pres elle est defini sur les endomorphisme de E...
oups autant pour moi, et désolé pour le pseudo ton peremptoire si tu l'as mal pris
j'ai mal lu la question
parcontre pas la peine d'écrire 50 lignes de morale pour me le dire nous sommes entre gentlemen :we:
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
