Problème d'algèbre (ou d'analyse ?)
24 messages
- Page 1 sur 2 - 1, 2
Problème d'algèbre (ou d'analyse ?)
Bonjour,
Je cherche à trouver la condition initiale "f(0)" de l'équation suivante :
f(x)= k.x / (a.f(x) + b) + f(0)
Les valeurs des constantes k, a et b sont connues.
Physiquement, cela correspond à l'évolution d'un courant I(t) dans un composant (inductance L) dont la valeur dépend de I(t). Malgré mes tentatives de révisions (équation du 2nd degré, équation fonctionnelle etc.), je suis toujours comme une poule qui a trouvé un couteau.
De ce fait, je suis attentif à vos suggestions.
Cordialement,
Quichenmath.
Je cherche à trouver la condition initiale "f(0)" de l'équation suivante :
f(x)= k.x / (a.f(x) + b) + f(0)
Les valeurs des constantes k, a et b sont connues.
Physiquement, cela correspond à l'évolution d'un courant I(t) dans un composant (inductance L) dont la valeur dépend de I(t). Malgré mes tentatives de révisions (équation du 2nd degré, équation fonctionnelle etc.), je suis toujours comme une poule qui a trouvé un couteau.
De ce fait, je suis attentif à vos suggestions.
Cordialement,
Quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
que savez-vous sur I(t). Dites-moi quels calculs vous avez essayé.
que savez-vous sur I(t). Dites-moi quels calculs vous avez essayé.
Re: Problème d'algèbre (ou d'analyse ?)
La description du problème est la suivante :
On applique un échelon de tension aux bornes d'une inductance (1 coup positif puis un coup négatif).
X volts pendant un temps DT et Y volts pendant un temps (1-D)T.
T = période et D = rapport cyclique.
Avec conservation des volts-secondes --> X.DT = Y.(1-D).T (en valeur abs).
En règle générale, on suppose une valeur du composant L = constante. Dans ce cas, la résolution est assez simple : I(t) = V.t / L + I0.
On sait que I(0) = I0 = Imin et que I(DT) = Imax. Chose que je n'ai pas précisé, on connait Imoyen.
Donc I0 = Imini = Imoyen - V.DT / (2.L)
Au final, on a une pente positive sur [0:DT] car X>0V et une pente négative sur [DT:(1-D)T] car Y<0V.
C'est à dire une ondulation "triangulaire" autour de la valeur moyenne.
Mais lorsqu'on souhaite prendre la caractéristique de L qui dépend du courant, L(I) = a.I(t)+b, j'éprouve des difficultés à résoudre l'équation.
J'ai essayé de trouver Imini avec la formule de calcul de la valeur moyenne (intégrale sur DT dans un 1er temps puis T ensuite,) --> 1 équation du 2nd degré, mais application numérique douteuse ..(résultats différents)
Intégrale sur DT :
--> Imoyen = I0 + 1/2 .(X.DT) / (a.I(t)+b)
--> si je pose I(t) = Imoyen, j'ai une équation du 2nd ordre à résoudre.
--> si je pose I(t) = I0, j'ai une équation du 2nd ordre à résoudre.
Mais poser I(t) = Imoyen ou I0 me pose problème vis à vis du sens physique.
Quichenmath.
On applique un échelon de tension aux bornes d'une inductance (1 coup positif puis un coup négatif).
X volts pendant un temps DT et Y volts pendant un temps (1-D)T.
T = période et D = rapport cyclique.
Avec conservation des volts-secondes --> X.DT = Y.(1-D).T (en valeur abs).
En règle générale, on suppose une valeur du composant L = constante. Dans ce cas, la résolution est assez simple : I(t) = V.t / L + I0.
On sait que I(0) = I0 = Imin et que I(DT) = Imax. Chose que je n'ai pas précisé, on connait Imoyen.
Donc I0 = Imini = Imoyen - V.DT / (2.L)
Au final, on a une pente positive sur [0:DT] car X>0V et une pente négative sur [DT:(1-D)T] car Y<0V.
C'est à dire une ondulation "triangulaire" autour de la valeur moyenne.
Mais lorsqu'on souhaite prendre la caractéristique de L qui dépend du courant, L(I) = a.I(t)+b, j'éprouve des difficultés à résoudre l'équation.
J'ai essayé de trouver Imini avec la formule de calcul de la valeur moyenne (intégrale sur DT dans un 1er temps puis T ensuite,) --> 1 équation du 2nd degré, mais application numérique douteuse ..(résultats différents)
Intégrale sur DT :
--> Imoyen = I0 + 1/2 .(X.DT) / (a.I(t)+b)
--> si je pose I(t) = Imoyen, j'ai une équation du 2nd ordre à résoudre.
--> si je pose I(t) = I0, j'ai une équation du 2nd ordre à résoudre.
Mais poser I(t) = Imoyen ou I0 me pose problème vis à vis du sens physique.
Quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
bonjour,
en faisant apparaitre un nombre dérivé, on obtient;
=\dfrac{k}{af(0)+b})
en faisant apparaitre un nombre dérivé, on obtient;
Modifié en dernier par mathelot le 22 Avr 2020, 16:49, modifié 1 fois.
Re: Problème d'algèbre (ou d'analyse ?)
J'ai essayé de comprendre votre démarche Mathelot (je n'ai pas l'esprit très vif en math  ).
).
Trouve-t-on cette relation en utilisant la dérivée composée u² --> 2u . u' ?
Si oui, je parviens à un résultat semblable : f'(0) = k / (2.a.f(0) + b).
Sinon, pouvez-vous m'indiquer la méthode utilisée ?
Après, il me restera à exploiter f'(0) pour trouver f(0).
Merci pour votre temps.
Quichenmath.
Trouve-t-on cette relation en utilisant la dérivée composée u² --> 2u . u' ?
Si oui, je parviens à un résultat semblable : f'(0) = k / (2.a.f(0) + b).
Sinon, pouvez-vous m'indiquer la méthode utilisée ?
Après, il me restera à exploiter f'(0) pour trouver f(0).
Merci pour votre temps.
Quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
vous écrivez "En règle générale, on suppose une valeur du composant L = constante. Dans ce cas, la résolution est assez simple : I(t) = V.t / L + I0"
L est constant , je suis d'accord, par contre I(t) = V.t / L + I0, j'ai un doute. En générale la tension aux bornes d'une bobine est de la forme V= L dans les phases transitoire c'est à dire quand la tension monte et descend ce qui arrive 3 fois pendant une période.
dans les phases transitoire c'est à dire quand la tension monte et descend ce qui arrive 3 fois pendant une période.
vous dites : "On sait que I(0) = I0 = Imin et que I(DT) = Imax. " est-ce une donnée?
vous écrivez "En règle générale, on suppose une valeur du composant L = constante. Dans ce cas, la résolution est assez simple : I(t) = V.t / L + I0"
L est constant , je suis d'accord, par contre I(t) = V.t / L + I0, j'ai un doute. En générale la tension aux bornes d'une bobine est de la forme V= L
vous dites : "On sait que I(0) = I0 = Imin et que I(DT) = Imax. " est-ce une donnée?
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
l'équation V=L signifie que en régime permanent il n'y plus de courant qui circule dans la bobine et donc la tension et aux bornes de la bobine est nulle.
signifie que en régime permanent il n'y plus de courant qui circule dans la bobine et donc la tension et aux bornes de la bobine est nulle.
vous écrivez : "X volts pendant un temps DT et Y volts pendant un temps (1-D)T. " je trouve cela très bizarre que la tension évolue pendant la période , même si le rapport cyclique n'est pas 1/2.
La bobine va alternativement se charger et se décharger en énergie magnétique. Question as-elle le temps de se charger ou se décharger entre 2 alternances?
l'équation V=L
vous écrivez : "X volts pendant un temps DT et Y volts pendant un temps (1-D)T. " je trouve cela très bizarre que la tension évolue pendant la période , même si le rapport cyclique n'est pas 1/2.
La bobine va alternativement se charger et se décharger en énergie magnétique. Question as-elle le temps de se charger ou se décharger entre 2 alternances?
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
En régime permanent, le courant dans la bobine est V/r ou V est la tension du générateur et r sa résistance interne ou en série.
En régime permanent, le courant dans la bobine est V/r ou V est la tension du générateur et r sa résistance interne ou en série.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
le "D" de DT est-il pour vous le même que dans (1-D)T.
votre système est périodique donc I(t0+T)=I(t0)
Si vous écrivez les équations de chaque phase de fonctionnement au cour d'une période. A la fin vous avez à résoudre I(t0+T)=I(t0)
le "D" de DT est-il pour vous le même que dans (1-D)T.
votre système est périodique donc I(t0+T)=I(t0)
Si vous écrivez les équations de chaque phase de fonctionnement au cour d'une période. A la fin vous avez à résoudre I(t0+T)=I(t0)
Re: Problème d'algèbre (ou d'analyse ?)
Merci pour ton temps Phyelec.
Le contexte est un convertisseur en électronique de puissance. En gros, on applique une tension rectangulaire de valeur moyenne nulle à une inductance qui est chargée par un générateur de courant (simule la charge). Dans le cas présent, on néglige la résistance interne de l'inductance.
Exemple de la tension rectangulaire du générateur :
70V pendant DT = 40% de la période (on magnétise l'inductance, le courant croît depuis Imin à Imax)
et -46.5 pendant (1-D)T = 60% de la période (on démagnétise l'inductance, le courant décroît de puis Imax à Imin).
(70V x 0.4) - (46.5V x 0.6) = 0V --> on a bien l'égalité des Volts-secondes et on se retrouve avec un courant de forme triangulaire. Le système est périodique (je raisonne en régime permanent).
Couramment, on prend la valeur de l'inductance L = cste. On obtient un courant de forme triangulaire dont la valeur moyenne est celle imposée par la charge. L'évolution est linéaire, il est facile de déduire Imin et Imax.
Ex : Imin = Icharge - V.0.5.DT/L et Imax = Icharge + V.0.5.DT/L.
En pratique, selon la technologie de l'inductance, la valeur de la self a tendance à réduire lorsque le courant croît et peut même saturer pour des courants trop importants (la fonction n'est plus linéaire).
De ce fait, mon courant croît selon une loi "parabolique" régit par ma valeur d'inductance qui est différente pour chaque "di" (--> je vais finir par conclure que j'ai une équation différentielle à résoudre .. :-\ )
Dans mon approche, j'ai remplacé le terme L=ctse par sa fonction L(I) = a.I(t)+b.
I(t) = V.t / L + Imin devient I(t) = V.t / (a.I(t)+b) + Imin et je me retrouve avec I(t) fonction de I(t) et je ne sais pas bien le "gérer". Ce n'est pas aussi intuitif que les droites du triangle.
Comme je suis médiocre en mathématique, je galère pour la résolution.
quichenmath
Le contexte est un convertisseur en électronique de puissance. En gros, on applique une tension rectangulaire de valeur moyenne nulle à une inductance qui est chargée par un générateur de courant (simule la charge). Dans le cas présent, on néglige la résistance interne de l'inductance.
Exemple de la tension rectangulaire du générateur :
70V pendant DT = 40% de la période (on magnétise l'inductance, le courant croît depuis Imin à Imax)
et -46.5 pendant (1-D)T = 60% de la période (on démagnétise l'inductance, le courant décroît de puis Imax à Imin).
(70V x 0.4) - (46.5V x 0.6) = 0V --> on a bien l'égalité des Volts-secondes et on se retrouve avec un courant de forme triangulaire. Le système est périodique (je raisonne en régime permanent).
Couramment, on prend la valeur de l'inductance L = cste. On obtient un courant de forme triangulaire dont la valeur moyenne est celle imposée par la charge. L'évolution est linéaire, il est facile de déduire Imin et Imax.
Ex : Imin = Icharge - V.0.5.DT/L et Imax = Icharge + V.0.5.DT/L.
En pratique, selon la technologie de l'inductance, la valeur de la self a tendance à réduire lorsque le courant croît et peut même saturer pour des courants trop importants (la fonction n'est plus linéaire).
De ce fait, mon courant croît selon une loi "parabolique" régit par ma valeur d'inductance qui est différente pour chaque "di" (--> je vais finir par conclure que j'ai une équation différentielle à résoudre .. :-\ )
Dans mon approche, j'ai remplacé le terme L=ctse par sa fonction L(I) = a.I(t)+b.
I(t) = V.t / L + Imin devient I(t) = V.t / (a.I(t)+b) + Imin et je me retrouve avec I(t) fonction de I(t) et je ne sais pas bien le "gérer". Ce n'est pas aussi intuitif que les droites du triangle.
Comme je suis médiocre en mathématique, je galère pour la résolution.
quichenmath
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
Je vois mieux votre problème.
vous dites "Dans mon approche, j'ai remplacé le terme L=ctse par sa fonction L(I) = a.I(t)+b", donc vous abandonnez le postulat L=Cste , Pourquoi ce revirement?
Je vois mieux votre problème.
vous dites "Dans mon approche, j'ai remplacé le terme L=ctse par sa fonction L(I) = a.I(t)+b", donc vous abandonnez le postulat L=Cste , Pourquoi ce revirement?
Re: Problème d'algèbre (ou d'analyse ?)
L'hypothèse L=cste est souvent suffisante en prenant une marge "pire-cas" de 20% par exemple sur Imax.
Dans le cas présent, je souhaite améliorer mon modèle analytique pour voir les effets de début de saturation et quantifier les pertes supplémentaires afin de mieux dimensionner mon dissipateur thermique (contraintes de masse et de volume). De plus, ce genre d'exercice met en évidence mes problèmes avec les mathématiques, matière dans laquelle je cherche à progresser (ce sont les maths qui limitent mes travaux en physique !).
La mise en équation et la résolution de ce problème m'intéressent particulièrement.
quichenmath.
Dans le cas présent, je souhaite améliorer mon modèle analytique pour voir les effets de début de saturation et quantifier les pertes supplémentaires afin de mieux dimensionner mon dissipateur thermique (contraintes de masse et de volume). De plus, ce genre d'exercice met en évidence mes problèmes avec les mathématiques, matière dans laquelle je cherche à progresser (ce sont les maths qui limitent mes travaux en physique !).
La mise en équation et la résolution de ce problème m'intéressent particulièrement.
quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
Moi je suis à l'aise en math et je connais un peu l'électronique, on peut chercher ensemble. Je vais réfléchir à la mise en équation. Dites mois ce que avez fait sur ce sujet.
Moi je suis à l'aise en math et je connais un peu l'électronique, on peut chercher ensemble. Je vais réfléchir à la mise en équation. Dites mois ce que avez fait sur ce sujet.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
Je dois partir au travail. Je prépare une petite synthèse et je l’édite ce soir.
Je suis parti sur les mêmes équations en remplaçant "L" par "a.I(t)+b".
Sur [0:DT] --> I(t) = V.t / (a.I(t)+b) + Imin. La valeur moyenne à priori, sur [0:DT] = Icharge.
En développant I(t), j'obtiens une équation du 2nd degré (A.I(t)²+B.I(t)+c=0) que je ne sais pas utiliser dans l'équation suivante : Icharge = (1/DT) INT(0-->DT) I(t).dt,
Bonne journée.
quichenmath.
Je dois partir au travail. Je prépare une petite synthèse et je l’édite ce soir.
Je suis parti sur les mêmes équations en remplaçant "L" par "a.I(t)+b".
Sur [0:DT] --> I(t) = V.t / (a.I(t)+b) + Imin. La valeur moyenne à priori, sur [0:DT] = Icharge.
En développant I(t), j'obtiens une équation du 2nd degré (A.I(t)²+B.I(t)+c=0) que je ne sais pas utiliser dans l'équation suivante : Icharge = (1/DT) INT(0-->DT) I(t).dt,
Bonne journée.
quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
Bonsoir,
J'ai trouvé un article qui évoque ma problématique. Je regarde si je peux en tirer quelque chose.
"Direct Modeling of Inductor Saturation Behavior in a SPICE Like Transient Analysis"
Lien :
https://www.google.fr/url?sa=t&rct=j&q= ... 0wT0L7x4x1
quichenmath.
J'ai trouvé un article qui évoque ma problématique. Je regarde si je peux en tirer quelque chose.
"Direct Modeling of Inductor Saturation Behavior in a SPICE Like Transient Analysis"
Lien :
https://www.google.fr/url?sa=t&rct=j&q= ... 0wT0L7x4x1
quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
Vous dites A.I(t)²+B.I(t)+c=0 donc I(t)=-(A.I(t)² +c)/B, remplacer dans
Icharge = dt = \dfrac{1}{DT}$\int_0^{DT} [-(A.I(t)^2 +c)/B] dt)
Vous dites A.I(t)²+B.I(t)+c=0 donc I(t)=-(A.I(t)² +c)/B, remplacer dans
Icharge =
Re: Problème d'algèbre (ou d'analyse ?)
Merci .
Je suis resté coincé sur mon équation du second degré ! Manque d'ouverture d'esprit ..
Je teste en application numérique et je vous tiens au courant.
Bonne soirée.
quichenmath.
Je suis resté coincé sur mon équation du second degré ! Manque d'ouverture d'esprit ..
Je teste en application numérique et je vous tiens au courant.
Bonne soirée.
quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
Je ne parviens pas à mettre en forme mon équation pour trouver une primitive de I²(t). Dois-je procéder par changement de variable ou une autre méthode ?
quichenmath.
Je ne parviens pas à mettre en forme mon équation pour trouver une primitive de I²(t). Dois-je procéder par changement de variable ou une autre méthode ?
quichenmath.
Re: Problème d'algèbre (ou d'analyse ?)
Bonjour,
Voici le calcul détaillé. Il faut que vous preniez le temps de réviser votre programme de math de terminale sur ce sujet.
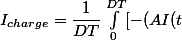^2 +c)/B ]dt)
soit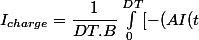^2 +c) ]dt)
soit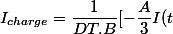^3 -c I(t) ]_0^{DT})
soit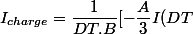^3 -c I(DT)+ \dfrac{A }{3}I(0)^3 +c I(0)])
Voici le calcul détaillé. Il faut que vous preniez le temps de réviser votre programme de math de terminale sur ce sujet.
soit
soit
soit
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
