Une suite vraiment pas mal...

[raito123]

bonjours,
pas d'introduction:
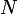
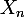
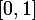
1/Montrer que pour tout n appartient à : admet une seul solution dans tel que:

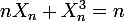
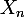
2/Montrer que la suite est croissante.
Voilà bonne chance.

[le_fabien]

bonsoir.
peux tu expliciter Xn ?

[le_fabien]

car pour Xn=1 il n'y a pas de probleme

[raito123]

C'est comme ça que l'exo est donné.
ET voici mon interpretation:
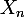
1/Dans la premiére question comme variable dans
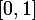
2/Dans la deuxiéme question elle represente une suite.
Je redis que c'est seulement ce que je pense mais la version original de l'exo c'est celle dans le premiere post.

[Nightmare]

Bonsoir,

je pense que l'exercice est plutot :

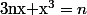
Montrer que l'équation admet une unique solution dans [0,1]. Montrer que la suite est croissante.

[le_fabien]

je pense comme Nightmare
en étudiant les variations de fn(x)=nx+x^3 on peut s'en sortir

[raito123]

Nightmare:
Tu peux donner une autre forme à l'exo, mais c'est comme ça qu'il est énoncé

[raito123]

je pense comme Nightmare
en étudiant les variations de fn(x)=nx+x^3 on peut s'en sortir

Je ne dis pas que la premiere question est difficile mais plutôt la deuxiéme.

[Nightmare]

Oui mais tel qu'il est donné, l'énoncé ne veut rien dire, le premier travail d'un étudiant devant un exercice est d'abord d'essayer de le décrypter.

[bruce.ml]

Tu peux interpreter comme tu veux raito mais l'enoncé que tu as donné n'a aucun sens. Ce n'est pas un prédicat mathématique !

[le_fabien]

sur [0;1] f'n(x)=n+3x²>0 donc fn est strictement croissante de plus fn(0)=0 et fn(1)=n+1
donc l'equation fn(x)=n admet une solution et unique

[Nightmare]

La deuxième question est triviale aussi.

On a
Alors :

D'où par différence :

Soit :

ie :

Or, vu que xn est à valeur dans [0,1] on a clairement 1-x(n+1) positif et le dénominateur aussi donc la suite est croissante.

:happy3:

[raito123]

Pour vous répondre j'ai mis du temps à analyser cet exo, et je me suis arreter au même point que vous donc Nightmare j'ai fais ce qu'il fallait faire.

[Skullkid]

Bonjour, on peut aussi le montrer de façon plus "élégante" en disant que , où . Comme est croissante sur [0,1] et que , on a immédiatement que .

[raito123]

Okey,je vois que c'est la bonne reponse.merci Nightmare
IL y a encore une question :
Montrer que :

[raito123]

Bonjour, on peut aussi le montrer de façon plus "élégante" en disant que , où . Comme est croissante sur [0,1] et que , on a immédiatement que .

Ah bon et comment donc tu donnes à

[Skullkid]

[Nightmare]

On a
D'où
Mais d'où
Et ainsi
ie

On en déduit de l'encadrement que (xn) converge vers 1.

[le_fabien]

faisons cette difference
Xn-(1-1/n)=(nXn-n+1)/n=(1-Xn^3)/n
sachant que Xn<1 on a Xn>1-1/n

[raito123]

Mais d'où (1)
Et ainsi (2)

Comment peut-on passer de (1) à (2).Je vois que je veux dire : qu'on ne peut pas dire que est superieur à