Une suite vraiment pas mal...

[Nightmare]

On a n+x(n)² < n+1 donc 1/(n+x(n)²) > 1/(n+1) d'où en multipliant par n :
n/(n+x(n)²) > n/(n+1) et tu n'auras pas de mal à montrer que n/(n+1) > 1-1/n

[raito123]

Je sais mais la partie qui m'intrigue c'est là voilà:
n+x(n)² < n+1 donc 1/(n+x(n)²) > 1/(n+1)

[Nightmare]

C'est la base ça non?

[raito123]

C'est parce que on ne peut pas dire que , non?

[Skullkid]

Ça on peut toujours le dire dès que n est supérieur à 1...

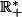
Cette étape du raisonnement de Nightmare s'appuie tout simplement sur la décroissance de la fonction inverse sur , et en effet c'est plutôt basique.