Petite règle et petit compas
42 messages
- Page 2 sur 3 - 1, 2, 3
Premièrement je reviens sur une consession que j'avais faite : on SAIT dans quelle section est B, on voit B, et on voit les droites qu'on a tracé, sinon comment peut on espérer joindre deux points qu'on ne voit pas. Au pire on met des gros drapeaux dessus. Dans les rêgles de construction à la rêgle et au compas, on sais où sont les points.
Sinon dans ce cas particulier, B est dans la grosse section d'angle, je trace donc la bissectrice qui part de A et qui va "en bas à droite". B est à présent dans la section de droite, je trace donc la bissectrice qui va vers "en haut à droite". La troisième étape devrait arriver près de B.
Sinon dans ce cas particulier, B est dans la grosse section d'angle, je trace donc la bissectrice qui part de A et qui va "en bas à droite". B est à présent dans la section de droite, je trace donc la bissectrice qui va vers "en haut à droite". La troisième étape devrait arriver près de B.
J'ai du mal à comprendre les conditions.
Si à partir d'une droite, on ne peut déterminer de quel coté se situe B, je ne vois pas comment on peut y arriver.
On peut toujours tracer deux droites à partir de A faisant un angle droit (ce qui fait 4 demi-droites) sur 150m environ de chaque coté. N'importe quelle droite issue de B rencontrera l'une de ces demi droites, ce qui permet de positionner B ?
Si à partir d'une droite, on ne peut déterminer de quel coté se situe B, je ne vois pas comment on peut y arriver.
On peut toujours tracer deux droites à partir de A faisant un angle droit (ce qui fait 4 demi-droites) sur 150m environ de chaque coté. N'importe quelle droite issue de B rencontrera l'une de ces demi droites, ce qui permet de positionner B ?
alben a écrit:J'ai du mal à comprendre les conditions . Si à partir d'une droite, on ne peut déterminer de quel coté se situe B, je ne vois pas comment on peut y arriver.
En fait on peut très bien y arriver mais on peut quand même dire que l'on sait de quel côté d'une droite se situe le point B . La question n'a jamais été posée aussi clairement et il est difficile de répondre "oui" à un message qui contient une vérité parmi de nombreuses contre-vérités . J'ajouterai qu'un message de raito123 trop vite oublié ne manque pas de pertinence .
Imod
Non mais c'est pas grave tu sais lmod si j'ai trouvé un autre moyen que le tien pour résoudre ce problème.
???????????????????????????????????????????????????
1+1 = 2. Youpie si un point est dans une section d'angle alors il est d'un certain coté des deux droites qui composent cet angle ! Ca sent la médaille Fields ça ...
lmod a écrit:La question n'a jamais été posée aussi clairement
lmod a écrit:Citation:
Posté par bruce.ml
3) on regarde dans quelle section d'angle est le point B
On n'en sait tout simplement rien
Imod
???????????????????????????????????????????????????
1+1 = 2. Youpie si un point est dans une section d'angle alors il est d'un certain coté des deux droites qui composent cet angle ! Ca sent la médaille Fields ça ...
Une petite mise au point sans animosité :we:
Une autre solution que la mienne serait un vrai plaisir j'ai depuis longtemps passé l'âge de telles mesquineries !
Il semblait d'après tes explications que tu enfermais d'emblée le point B dans un angle de sommet A en "visant B" ce qui n'est pas tout à fait la même chose que de dire "B est de tel côté d'une droite" , d'où le schéma proposé et les explications demandées . Bon disons que nous sommes d'accord : on peut tracer une droite (D) passant par A telle que d(B,(D))<d .
Jusqu'ici pas de problème .
Je ne vois pas comment fonctionne la récursivité les milieux de [AC] et [BF] ne semblant pas constructibles à priori . En attendant ta réponse , tu me permettras de suspendre momentanément l'attribution de la médaille Fields :we:
Imod
bruce.ml a écrit:Non mais c'est pas grave tu sais lmod si j'ai trouvé un autre moyen que le tien pour résoudre ce problème.
Une autre solution que la mienne serait un vrai plaisir j'ai depuis longtemps passé l'âge de telles mesquineries !
bruce.ml a écrit:Youpie si un point est dans une section d'angle alors il est d'un certain coté des deux droites qui composent cet angle ! Ca sent la médaille Fields ça ...
Il semblait d'après tes explications que tu enfermais d'emblée le point B dans un angle de sommet A en "visant B" ce qui n'est pas tout à fait la même chose que de dire "B est de tel côté d'une droite" , d'où le schéma proposé et les explications demandées . Bon disons que nous sommes d'accord : on peut tracer une droite (D) passant par A telle que d(B,(D))<d .
bruce.ml a écrit:Plaçons un point C sur cette droite, à distance moins de d de B, et plus proche de A que B ne l'est ; et un point D toujours sur la droite à distance moins de d de C. O, sait construire le parlallélogramme CDBE, et la demi droite [BE). Par suite on sait construire le parallélogramme ACBF. On a que le milieu de [AB] est le milieu du milieu de [AC] et du milieu de [FB]. Si on a le milieu de [AB], nous avons un procédé recursif pour construire notre segment à base de milieux successifs.
Jusqu'ici pas de problème .
bruce.ml a écrit:Et pour obtenir ce dernier, il suffit d'avoir les milieux de deux segments : [AC] et [FB] qui sont de longueur plus petite que celle de [AB]. En procédant récursivement, et grace à cet algorithme en complexité doublement exponentielle, on arrivera à tracer le segment [AB] !
Je ne vois pas comment fonctionne la récursivité les milieux de [AC] et [BF] ne semblant pas constructibles à priori . En attendant ta réponse , tu me permettras de suspendre momentanément l'attribution de la médaille Fields :we:
Imod
Nous y voilà ! c'est quand même mieux quand tu me dis où tu penses que ça ne va pas :++: La récursivité fonctionne car AC = BF < AB
Mon premier objectif était de construire le milieu de [AB], j'ai ramené le problème à la construction du milieu d'un segment plus petit. Au bout d'un moment le segement sera assez petit pour qu'on puisse le tracer et construire son milieu grace à une médiatrice par exemple :)
Mon premier objectif était de construire le milieu de [AB], j'ai ramené le problème à la construction du milieu d'un segment plus petit. Au bout d'un moment le segement sera assez petit pour qu'on puisse le tracer et construire son milieu grace à une médiatrice par exemple :)
bruce.ml a écrit:La récursivité fonctionne car AC = BF < AB . Mon premier objectif était de construire le milieu de [AB], j'ai ramené le problème à la construction du milieu d'un segment plus petit. Au bout d'un moment le segement sera assez petit pour qu'on puisse le tracer et construire son milieu grace à une médiatrice par exemple
Désolé , je suis bouché ( je ne fais pas de l'obstruction ) . Au départ tu vises le point B que vises-tu après :mur: :mur: :mur:
Imod
Bon je recommence l'algorithme avec tous les points, cet algorithme cherche à tracer le milieu de deux points.
d est la distance dans laquelle on peut travailler avec la rêgle et le compas de façon normale ( mettons 30 cm )
0) Soient A et B les deux points à relier. si d(A,B) < d, tracer le segment [A,B], puis son milieu grace à sa médiatrice, et terminer.
1) Tracer deux droites passant par A et le cercle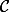 de centre B et de rayon d/2.
de centre B et de rayon d/2.
2) Si une droite passe par deux points distincs de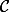 , nomons les C et D, C étant le plus proche de A, et aller en 4)
, nomons les C et D, C étant le plus proche de A, et aller en 4)
3) Tracer la bissectrice interieure de l'angle contenant le point B, aller en 2)
4) Le point E est tel que CDBE est un parallélogramme, tracer la droite [BE). Elle coupe le cercle de centre A et de rayon d en deux points, F et G, F étant le plus proche de B.
5) Construire récursivement les milieux H et I de [AC] et [FB]
6) tracer le segement [HI] et construire son milieu grace à une mediatrice : c'est le milieu de [AB] et terminer.
( Si on peut prouver que FC < AB, on peut simplement appeller recursivement le milieu de [FC] à la place des étapes 5 et 6 )
Après ça on construit récursivement tous les milieux des milieux des milieux ... jusqu'à arriver à des longueurs traçables avec notre rêgle
d est la distance dans laquelle on peut travailler avec la rêgle et le compas de façon normale ( mettons 30 cm )
0) Soient A et B les deux points à relier. si d(A,B) < d, tracer le segment [A,B], puis son milieu grace à sa médiatrice, et terminer.
1) Tracer deux droites passant par A et le cercle
2) Si une droite passe par deux points distincs de
3) Tracer la bissectrice interieure de l'angle contenant le point B, aller en 2)
4) Le point E est tel que CDBE est un parallélogramme, tracer la droite [BE). Elle coupe le cercle de centre A et de rayon d en deux points, F et G, F étant le plus proche de B.
5) Construire récursivement les milieux H et I de [AC] et [FB]
6) tracer le segement [HI] et construire son milieu grace à une mediatrice : c'est le milieu de [AB] et terminer.
( Si on peut prouver que FC < AB, on peut simplement appeller recursivement le milieu de [FC] à la place des étapes 5 et 6 )
Après ça on construit récursivement tous les milieux des milieux des milieux ... jusqu'à arriver à des longueurs traçables avec notre rêgle
Imod a écrit:Inutile de noyer le poisson , le problème est là ( je garde toujours la médaille sous le coude :we: )
Imod
Au temps pour moi ! il faut ajouter une petite condition supplémentaire : à l'étape deux, si
PS : le premier algorithme était probabiliste et terminait avec une probabilité de 1 :p.
bruce.ml a écrit:d/2 est facilement constructible avec une simple médiatrice de toute façon
Ben je vois pas comment tu mesure d. Si tu me dit qu'il faut prendre les extrémités de ta regles je te previens tout de suite que je me gausse ! On sait tous que les bords d'une regle sont arrondies (ou usés rapidement si ils étaient pas arrondies) ! Mais de toute facon n'importe quelle longueur témoin inférieur à d fait l'affaire.
Patastronch a écrit:Ben je vois pas comment tu mesure d. Si tu me dit qu'il faut prendre les extrémités de ta regles je te previens tout de suite que je me gausse ! On sait tous que les bords d'une regle sont arrondies (ou usés rapidement si ils étaient pas arrondies) ! Mais de toute facon n'importe quelle longueur témoin inférieur à d fait l'affaire.
voilà n'importe quel d > 0 convient du moment qu'il est plus petit que la rêgle.
En effet la construction aboutit un peu laborieusement mais sûrement . La précision risque de ne pas être au rendez-vous mais l'exercice est plus théorique que pratique !
Une autre façon de faire qui me semble plus simple . On quadrille une partie finie du plan contenant A et B avec des carrés suffisamment petits pour permettre de mesurer l'écart entre deux points ( au compas ) ou pour relier deux points ( à la règle ) , dans deux carrés voisins et de façon à ce que A soit un noeud du quadrillage . On place alors un point dans chaque carré ne contenant pas B et par ces points on trace une ligne brisée reliant A à B . La trajectoire complète est contenue dans un carré nXn , on la reproduit à l'echelle 1/n dans le premier carré partant de A et en reliant A au dernier point de la trajectoire réduite , on obtient ( théoriquement ) la direction de B .
Imod
PS : bruce.ml , pour la médaille Fields , je verrai ce que je peux faire mais je ne peux rien te certifier :we:
Une autre façon de faire qui me semble plus simple . On quadrille une partie finie du plan contenant A et B avec des carrés suffisamment petits pour permettre de mesurer l'écart entre deux points ( au compas ) ou pour relier deux points ( à la règle ) , dans deux carrés voisins et de façon à ce que A soit un noeud du quadrillage . On place alors un point dans chaque carré ne contenant pas B et par ces points on trace une ligne brisée reliant A à B . La trajectoire complète est contenue dans un carré nXn , on la reproduit à l'echelle 1/n dans le premier carré partant de A et en reliant A au dernier point de la trajectoire réduite , on obtient ( théoriquement ) la direction de B .
Imod
PS : bruce.ml , pour la médaille Fields , je verrai ce que je peux faire mais je ne peux rien te certifier :we:
42 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

