Fonction zêta de Riemann

par **euclide** » 17 Oct 2007, 15:04

Bonjour à tous, voilà un exo qui me pose problème, si vous pouvez m'aidez...

--> Il faut montrer que la fonction :

est analytique sur C pour n>0.

--> Il faut montrer que la série

converge uniformément sur : {

pour

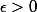
-->De même qu'elle converge normalement sur {

par **kazeriahm** » 17 Oct 2007, 18:40

salut

pour le premier il suffit d'utiliser le développement de l'exponentielle en série entière (ou plus simplement de voir que ta fonction est holomorphe)

par **euclide** » 19 Oct 2007, 18:55

Merci, mais je vois pas le lien avec l'exponentielle. On peut en effet écrire cette fonction avec l'exponentielle, mais alors on a besoin d'une détermination du logarithme et on ne peut plus dire qu'elle est analytique sur C entier non ??? Je ne sais pas si je fais bonne route...

par **Mohamed** » 19 Oct 2007, 21:18

c'est quoi analytique sur C?

par **Joker62** » 20 Oct 2007, 01:54

Exprimable localement sous la forme d'une série entière convergente

par **quinto** » 20 Oct 2007, 02:29

Joker62 a écrit:Exprimable localement sous la forme d'une série entière convergente

Globalement puisqu'elle est analytique sur C

Pour le coup de l'exponentielle, non on n'a pas besoin d'une détermination du logarithme, vu que n^z=exp(zln(n)) on prend le log d'un entier et donc il n'y a pas de souci à se faire, la variable complexe est z.

a+

Fonction zêta de Riemann

Fonction zêta de Riemann

Qui est en ligne