Fonction zêta de Riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 17 Juil 2017, 16:54
par mehdi-128 » 17 Juil 2017, 16:54
Bonjour,
La fonction zêta est définie sur ]1,+inf[ par
=\sum_{n=1}^{+\infty}\frac{1}{n^x})
On note pour n entier naturel non nul et x réel >1 :
 = \sum_{k=n+1}^{+\infty}\frac{1}{k^x}=\zeta(x)-\sum_{k=1}^{n}\frac{1}{k^x})
Montrer que pour tout entier naturel non nul et x réel x>1 :
 \leq \frac{1}{(x-1)n^{x-1}})
Je vois pas par où commencer...
-
aviateur
 par aviateur » 17 Juil 2017, 17:11
par aviateur » 17 Juil 2017, 17:11
Bonjour
Je crois qu'il faut que tu vois que 1/k^x est plus petit qu'une intégrale qui va de k-1 à k ou bien k à k+1
(fais un petit dessin)
de la fonction 1/u^x.
Avec cela tu pourras majorer ton reste par une intégrale qui va jusque + l'infini et facile à calculer. Normalement
tu tombes sur ce qu'il faut.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 17 Juil 2017, 20:18
par mehdi-128 » 17 Juil 2017, 20:18
aviateur a écrit:Bonjour
Je crois qu'il faut que tu vois que 1/k^x est plus petit qu'une intégrale qui va de k-1 à k ou bien k à k+1
(fais un petit dessin)
de la fonction 1/u^x.
Avec cela tu pourras majorer ton reste par une intégrale qui va jusque + l'infini et facile à calculer. Normalement
tu tombes sur ce qu'il faut.
J'ai fait un dessin et après je vois pas trop.

-
Arbre
 par Arbre » 18 Juil 2017, 12:11
par Arbre » 18 Juil 2017, 12:11
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 19 Juil 2017, 15:23
par mehdi-128 » 19 Juil 2017, 15:23
EN gros j'ai
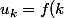 = \frac{1}{k^x})
Je prends un entier k non nul et t appartenant à [k-1,k] :

f est décroissante sur [1,+inf[ donc :
 \leq f(t) \leq f(k-1))
 \leq \int_{k-1}^{k} f(t)dt)
Donc :
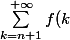 \leq \sum_{k=n+1}^{+\infty}\int_{k-1}^{k} f(t)dt = \int_{n}^{+\infty} \frac{1}{t^x}dt)
Enfin :
 \leq \int_{n}^{+\infty} t^{-x}dt)
L'intégrale de droite se calcule facilement et on obtient le résultat c'est bien ça ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités