Enigme des 4 4
Olympiades mathématiques, énigmes et défis
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 28 Nov 2005, 07:55
par Patastronch » 28 Nov 2005, 07:55
euh pour moi ca fait bien 40 ...
4*4=16
4!=24
16+24=40
40/4=10
...
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 30 Nov 2005, 16:48
par Patastronch » 30 Nov 2005, 16:48
Bon je suis arrivé jusqu'a 72, je les mets pas j ai la flem. Par contre je bloque sur le 73. Je me demande meme si c'est possible.
-
scelerat
- Membre Relatif
- Messages: 397
- Enregistré le: 03 Aoû 2005, 13:37
-
 par scelerat » 01 Déc 2005, 15:32
par scelerat » 01 Déc 2005, 15:32
Patastronch a écrit:Bon je suis arrivé jusqu'a 72, je les mets pas j ai la flem. Par contre je bloque sur le 73. Je me demande meme si c'est possible.
Je suis bloque des 41. Peut-etre que si tu nous donnes quelques uns des impairs entre 41 et 69 que tu as trouve, ca nous donnera des idees...
-
scelerat
- Membre Relatif
- Messages: 397
- Enregistré le: 03 Aoû 2005, 13:37
-
 par scelerat » 01 Déc 2005, 17:12
par scelerat » 01 Déc 2005, 17:12
Patastronch a écrit:Bon je suis arrivé jusqu'a 72, je les mets pas j ai la flem. Par contre je bloque sur le 73. Je me demande meme si c'est possible.
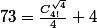
Pour les autres, j'ai une solution admirable que cette page est malheureusement trop petite pour contenir ... :++:
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 02 Déc 2005, 00:44
par Patastronch » 02 Déc 2005, 00:44
41 = (4*4 + .4) / .4
(le .x correspond en notation anglaise à 0,x)
-
scelerat
- Membre Relatif
- Messages: 397
- Enregistré le: 03 Aoû 2005, 13:37
-
 par scelerat » 02 Déc 2005, 09:07
par scelerat » 02 Déc 2005, 09:07
Patastronch a écrit:41 = (4*4 + .4) / .4
(le .x correspond en notation anglaise à 0,x)
:id:
J'aurais du y penser, j'ai introduit le

avec comme alibi que la notation anglaise ne faisait intervenir que des parentheses
)
!
-
sidani
- Messages: 7
- Enregistré le: 20 Sep 2007, 13:07
-
 par sidani » 03 Oct 2007, 10:50
par sidani » 03 Oct 2007, 10:50
eraule a écrit:20 = 4*(4+4/4)
je sais c'était facile...
je rajoute ceux là :
21 = 4! - ((4)^1/2 + 4/4)
22 = 4!-(4/4)(4^1/2)
23 = ((4*4)^1/2)!)-4/4
24 = 4*4 + 4 + 4 = 4*4 + 4(4)^1/2 = (4/4)*((4*4)^1/2)!)
25 = ((4*4)^1/2)!)+4/4
26 = 4!+(4/4)(4^1/2)
27 = 4! + ((4)^1/2 + 4/4)
28 = 4!+4*4/4
29 = 4!+4+4/4
30 = 4! + (4*4)^1/2 + 4^1/2
quand tu en as un, tu les as tous, c'est assez agréable comme exercice...
je vois l:1;2 il n'ai pas possible
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 03 Oct 2007, 17:33
par Imod » 03 Oct 2007, 17:33
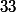
sans les

ou
)
:
^{4!}+\sqrt{4}}{\sqrt{4}})
Imod
PS :
un lien intéressant sur le même sujet .
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 04 Oct 2007, 01:48
par Patastronch » 04 Oct 2007, 01:48
:doh:
Fallait en vouloir pour le pondre celui la !
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 04 Oct 2007, 16:53
par Imod » 04 Oct 2007, 16:53
Patastronch a écrit::doh: Fallait en vouloir pour le pondre celui la !
Tu ne l'avais pas trouvé ? Pourtant facile :technicol :arf2:

:dingue:
Imod
-
oufi
- Messages: 6
- Enregistré le: 05 Oct 2007, 15:52
-
 par oufi » 05 Oct 2007, 16:08
par oufi » 05 Oct 2007, 16:08
ça veux dire koi "!"
par exemple 4!=24 ???
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 05 Oct 2007, 16:24
par Patastronch » 05 Oct 2007, 16:24
oufi a écrit:ça veux dire koi "!"
par exemple 4!=24 ???
Pour tout n entier naturel :
n! = n * (n-1) * (n-2) * ... * 1
avec pour convention 0! = 1
n! se lit factorielle n (meme si tout le monde dit n factorielle)
exemple : 4! = 4 * 3 * 2 * 1 = 24
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 05 Oct 2007, 16:34
par Patastronch » 05 Oct 2007, 16:34
attention a ne pas confondre avec la multifactorielle :
n!! = n * (n-2) * (n-4) ...
(n!)! different de n!!
-
oufi
- Messages: 6
- Enregistré le: 05 Oct 2007, 15:52
-
 par oufi » 05 Oct 2007, 16:35
par oufi » 05 Oct 2007, 16:35
oki oki merci :)
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 05 Oct 2007, 23:19
par bruce.ml » 05 Oct 2007, 23:19
multifactorielle ça n'existe pas ça :P
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 06 Oct 2007, 00:49
par Patastronch » 06 Oct 2007, 00:49
-
FlyGhost
- Messages: 9
- Enregistré le: 29 Sep 2007, 14:09
-
 par FlyGhost » 06 Oct 2007, 08:27
par FlyGhost » 06 Oct 2007, 08:27
Savai pas pour la multi! interessant merci :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
