Primitive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
hec
- Membre Naturel
- Messages: 37
- Enregistré le: 30 Sep 2006, 16:51
-
 par hec » 29 Aoû 2007, 20:22
par hec » 29 Aoû 2007, 20:22
Bonjour,
Pouvez-vous m'aider à trouver une primitive de racine de (t-1) ?
J'avais pensé faire un changement de variable en posant u²=t-1 mais je trouve comme primitive (2/3)u^3 et ça cloche.
Merci !
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
 par Mohamed » 29 Aoû 2007, 20:25
par Mohamed » 29 Aoû 2007, 20:25
f(t)=racine(t-1)=(t-1)^(1/2) donc 2/3*(t-1)^(3/2) est une primitive de f
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 29 Aoû 2007, 20:31
par barbu23 » 29 Aoû 2007, 20:31
Bonjour "hec" :
On a :
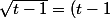'.(t-1)^{\frac{1}{2}} $)

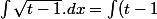'.(t-1)^{\frac{1}{2}}.dx + cte = \frac{.(t-1)^{\frac{1}{2}+1}}{\frac{1}{2}+1} + cte $)
avec

.
-
hec
- Membre Naturel
- Messages: 37
- Enregistré le: 30 Sep 2006, 16:51
-
 par hec » 29 Aoû 2007, 20:34
par hec » 29 Aoû 2007, 20:34
salut, merci pour ta réponse !
Mais si je dérive ta primitive, je ne retombe pas sur racine (t-1) !
2/3*(t-1)^(3/2)=2/3*(t-1)*racine de (t-1)
en posant u(t)=2(t-1)/3
u'(t)=2/3
v(t)= racine de (t-1)
v'(t) = 1/(racine de t-1)
u'v+v'u= 4/3*racine de (t-1) !
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
 par Mohamed » 29 Aoû 2007, 20:44
par Mohamed » 29 Aoû 2007, 20:44
(u^r)'=r*u^(r-1)*u' !
-
hec
- Membre Naturel
- Messages: 37
- Enregistré le: 30 Sep 2006, 16:51
-
 par hec » 29 Aoû 2007, 20:52
par hec » 29 Aoû 2007, 20:52
Mohamed a écrit:(u^r)'=r*u^(r-1)*u' !
Oui avec r un entier naturel non nul !
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 29 Aoû 2007, 20:54
par quinto » 29 Aoû 2007, 20:54
hec a écrit:Oui avec r un entier naturel non nul !
Non, avec r constant. Peu importe qu'il soit entier non nul ou pas.
-
hec
- Membre Naturel
- Messages: 37
- Enregistré le: 30 Sep 2006, 16:51
-
 par hec » 29 Aoû 2007, 20:58
par hec » 29 Aoû 2007, 20:58
Finalement moi je dis qu'une primitive de racine de (t-1) c'est 1/2*(t-1)^(3/2)
car si on redérive ça en posant :
u(t)=(t-1)/2
u'(t)=1/2
v(t)= racine de (t-1)
v'(t) = 1/(racine de t-1)
u'v+v'u= 1/2*racine de (t-1) + 1/(racine de t-1)*(t-1)/2
=1/2*racine de (t-1) + 1/2*racine de (t-1)
= racine de (t-1) !
-
hec
- Membre Naturel
- Messages: 37
- Enregistré le: 30 Sep 2006, 16:51
-
 par hec » 29 Aoû 2007, 21:00
par hec » 29 Aoû 2007, 21:00
quinto a écrit:Non, avec r constant. Peu importe qu'il soit entier non nul ou pas.
Pourquoi alors quand je redérive 1/2*(t-1)^(3/2), je retombe sur racine de (t-1) ? voir cidessus.
et quand je redérive votre proposition non ?
Où est mon erreur ?
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 29 Aoû 2007, 21:23
par Edrukel » 29 Aoû 2007, 21:23
tout ce qui trouble ton cerveau c'est de ne pas savoir ton cours lol :-)
on a :: v'(t)=1/(2*racine de t-1) et non v'(t) = 1/(racine de t-1)
voilà,avec mes respects pour toi
-
hec
- Membre Naturel
- Messages: 37
- Enregistré le: 30 Sep 2006, 16:51
-
 par hec » 29 Aoû 2007, 21:27
par hec » 29 Aoû 2007, 21:27
Edrukel a écrit:tout ce qui trouble ton cerveau c'est de ne pas savoir ton cours lol

on a :: v'(t)=1/(2*racine de t-1) et non v'(t) = 1/(racine de t-1)
voilà,avec mes respects pour toi
:mur:
Merci à toi Edrukel !
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 29 Aoû 2007, 21:52
par Edrukel » 29 Aoû 2007, 21:52
de rien hec
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
