Un petit prob de stats

[titiraf]

Bonjour,
Je voudrais vous soumettre ce problème :
Je souhaite attribuer une note à des sujets en fonction d'un résultat A
Je considère que le résultat A : 8/3 c'est à dire 2.67 vaut 20/20
On fait l'hypothèse que plus on s'éloigne de ce critère plus la note sera basse. C'est ainsi qu'un résultat de 2.81 vaudra 18.98/20.
Donc il ne s'agit pas ici de faire une règle de 3. puisque que la note est inversement proportionnel à A.
Le problème est que parfois le résultat A est si bas que la note calculée dépasse le 20/20. C'est le cas de 2.53 qui donne une note de 21.11.
Quelqu'un pourrait-il me dire ce que je pourais faire pour éviter d'aboutir à un tel résultat.
Je vous remercie infiniment de votre aide.
Cordialement
THIERRY

[anima]

Bonjour,
Je voudrais vous soumettre ce problème :
Je souhaite attribuer une note à des sujets en fonction d'un résultat A
Je considère que le résultat A : 8/3 c'est à dire 2.67 vaut 20/20
On fait l'hypothèse que plus on s'éloigne de ce critère plus la note sera basse. C'est ainsi qu'un résultat de 2.81 vaudra 18.98/20.
Donc il ne s'agit pas ici de faire une règle de 3. puisque que la note est inversement proportionnel à A.
Le problème est que parfois le résultat A est si bas que la note calculée dépasse le 20/20. C'est le cas de 2.53 qui donne une note de 21.11.
Quelqu'un pourrait-il me dire ce que je pourais faire pour éviter d'aboutir à un tel résultat.
Je vous remercie infiniment de votre aide.
Cordialement
THIERRY

Prendre une fonction de répartition avec comme maximum 2.67? Une cloche de Gauss pourrait bien marcher dans ce cas la... Quelque chose du genre . Il te reste a définir pour que f(2.81)=18.98 :ptdr:

[jm69]

Bonjour Anima,

3 minutes pour résoudre ce problème... vous êtes plutôt doué.

pourriez-vous m'aider SVP? j'ai posté ma question à l'adresse suivante :

http://www.maths-forum.com/showthread.php?t=39040

Merci !

[Isomorphisme]

Bonjour,

Titiraf, je ne comprends pas bien le système. Si un individu a moins de 8/3, pourquoi ne pas lui attribuer 20 (il s'agit donc d'une note tronquée) ? Car la solution proposée par Anima ne me semble pas adaptée car un individu s'éloignant de 8/3 (à gauche) aura une note toujours inférieure à 20 (quel que soit l'écart-type du reste). Or j'imagine bien que l'individu qui a moins que 8/3 a fait une meilleure performance que celui qui a fait 8/3 exactement ?

La note sur 20 vérifie actuellement d'après ton critère :

où note est la note observée. Et donc en tronquant la note à 20, la formule devient :

[anima]

Bonjour,

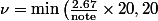Titiraf, je ne comprends pas bien le système. Si un individu a moins de 8/3, pourquoi ne pas lui attribuer 20 (il s'agit donc d'une note tronquée) ? Car la solution proposée par Anima ne me semble pas adaptée car un individu s'éloignant de 8/3 (à gauche) aura une note toujours inférieure à 20 (quel que soit l'écart-type du reste). Or j'imagine bien que l'individu qui a moins que 8/3 a fait une meilleure performance que celui qui a fait 8/3 exactement ?

Justement non, son probleme est que 2.67 est le "maximum absolu". Tout ecart a gauche ou a droite, si j'ai bien compris, est moins bien.

[Isomorphisme]

Ah donc si c'est bien ça, oui je suis d'accord avec toi anima. La gaussienne est une solution simple possible.

[anima]

Ah donc si c'est bien ça, oui je suis d'accord avec toi anima. La gaussienne est une solution simple possible.

Sinon, encore plus simple, une fonction polynome de degre pair avec comme maximum 2.67. L'inconvenient, on aura ainsi des notes negatives. L'avantage, les notes seront directement proportionnelles.

[titiraf]

Un grand merci à tous pour avoir réfléchi à mon problème.
Mais comment faire concrètement pour obtenir la note.
quel est l'équation avec l'inconnu pour obtenir cette note.
Merci

[anima]

Un grand merci à tous pour avoir réfléchi à mon problème.
Mais comment faire concrètement pour obtenir la note.
quel est l'équation avec l'inconnu pour obtenir cette note.
Merci

En prenant comme j'ai dit une Gaussienne:


f(2.81) = 18.98
Donc
(Un ecart-type est toujours positif...)
Soit ... avec x la note ~ 2.67, et f(x) sa note sur 20.