Probleme d'intégration

par **audre66** » 14 Juin 2007, 09:58

bonjour
j'ai f(x)=1§x ln(1+t)/t dt
et je doit montrer que f(x) est C1 et que f(x) + f(1/x)=(lnx)^2/2
je vois pas ce qu'est C1 et je n'arrive pas a intégrer si vous pourriez m'aidar ce serai génial
merci

par **Bodyboard.Pro-Rider>Vert** » 14 Juin 2007, 10:09

f(x) + f(1/x)=(lnx)^2/2

Bonjour,pour le calcul (dans f(1/x)) :pose le changement de variable:u=1/t =>du=(-dt)/t^2
tu devrais t'en sortir.......

par **audre66** » 14 Juin 2007, 10:19

tu te trompe c pas ça que je doi intégrer

par **Bodyboard.Pro-Rider>Vert** » 14 Juin 2007, 11:12

???Je comprends pas ton raisonnement.

par **thomasg** » 14 Juin 2007, 11:34

ln(1+t)/t est continue sur [1;+inf[ donc f est C1 (demande si tu veux la preuve du théorème utilisé).

A bientôt.

par **thomasg** » 14 Juin 2007, 11:54

Il n'est pas nécessaire d'intégrer il me semble.

Tout d'abord on peut constater que les deux fonctionsf
f(x) + f(1/x) et (lnx)^2/2 prennent la même valeur en 1.

Ensuite on va montrer qu'elles ont la même dérivée, elles seront donc égales.

(f(x)+f(1/x))'=f'(x)-f'(1/x)/x²=(ln(1+x))/x-ln(1+1/x)*x/x²=ln(x)/x

de même

[(lnx)^2/2]'=ln(x)/x

(Démo à vérifier)

A bientôt.

par **audre66** » 14 Juin 2007, 12:57

mais C1 c quoi?

par **audre66** » 14 Juin 2007, 13:08

je trouve pas qu'en 1 il est la meme valeur

par **thomasg** » 14 Juin 2007, 13:13

C1 c'est: dérivable et à dérivée continue

f(1)=1§1(....)=0
f(1/1)=1§1/1(.....)=0

ln(1)^2/2=0

f(1)+f(1/1)=ln(1)^2/2

En 1 elles ont donc bien la même valeur.

par **audre66** » 14 Juin 2007, 13:16

et je comprend pas commment tu dérive f(x)et f(1/x)

par **thomasg** » 14 Juin 2007, 13:34

Tu utilises la propriété suivante (le f qui y figure n'est pas celui de ton énoncé):

[0§x(f(t)dt)]'=f(x)

(propriété applicable ici: on a montré que la fonction était C1)

par **audre66** » 14 Juin 2007, 13:34

stp aide moi je comprend pas commeznt on dérive ce genre de fontion

par **audre66** » 14 Juin 2007, 13:40

ok mais je vois toujours pas comment on arrive a ce que tu m'as écrit avant

par **audre66** » 14 Juin 2007, 13:42

pourquoi est ce qu'on dérive deux vu que F(x)'=f(x)

par **thomasg** » 14 Juin 2007, 13:51

Je n'ai pas été très judicieux en te proposant la propriété avec la lettre f, la voilà réécrite:

[0§x(g(t)dt)]'=g(x)

ce qui donne ici:

[0§x(ln(1+t)/t dt]'=ln(1+x)/x

par **audre66** » 14 Juin 2007, 14:07

dans ce cas ma dérivé est = ln(1+x)/x + ln(1+1/x)/x somme nous d'accord?

par **thomasg** » 14 Juin 2007, 14:31

ln(1+x)/x - ln(1+1/x)/x

car la dérivée de 1/x est -1/x². (ne pas oublier d'appliquer la formule de dérivée des fonctions composées)

par **audre66** » 14 Juin 2007, 14:34

bon attend soit je suis vraiment bete soit on se comprend pas tu me di que F(x)'=f(x) donc on ne dérive pas et la tu dérive je comprend pas

par **Pythales** » 14 Juin 2007, 15:05

Je pose

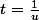
ce qui donne après quelques transformations

soit

par **thomasg** » 14 Juin 2007, 15:14

[f(1/x)]'=(-1/x²)f '(1/x)=-1/x²(ln(1+1/x)/(1/x))=-(ln(1+1/x)/x

(formule de dérivation des fonctions composées.

Probleme d'intégration

probleme d'intégration

Qui est en ligne