Recherche de fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Giansolo
- Membre Naturel
- Messages: 44
- Enregistré le: 02 Fév 2007, 14:38
-
 par Giansolo » 15 Mar 2007, 10:53
par Giansolo » 15 Mar 2007, 10:53
Bonjour tout le monde,
Ce post fais suite au topic "
Fittage de courbe par des fcts exponentielles".
Je tiens tout d'abord à remercier ces personnes qui m'ont aidées sur le topic précédent avec de la bonne humeur (devant mes questions un peu bêtes).
Mon problème a aujourd'hui légèrement évolué, et je cherche (en simplifiant) à fittter un ensemble de points avec une fonction exponentielles concave ou convexe, croissante ou décroissante, soit une fonction qui puisse prendre chacune des formes suivantes (un "OU" exclusif: soit cette forme la, soit l'autre, mais pas un mélange de deux formes) :

J'aimerais pouvoir attaquer ce fittage comme dans le topic précédent, avec une régréssion logarithmique, est-ce que c'est possible ? et Quelles sont les pistes à suivre ?
Merci!
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 15 Mar 2007, 12:53
par Quidam » 15 Mar 2007, 12:53
J'étais passé complètement à côté du fil auquel tu fais référence ! Je viens de le lire en diagonale... Je ne vois absolument rien de nouveau ici. Qui peut le plus peut le moins. Je pense que tu as eu toutes les explications nécessaires dans ce fil, et si tu sais "fitter" une courbe formée de plusieurs morceaux d'exponentielles, tu sais alors "fitter" une courbe formée d'un seul !
Dès l'instant que tu soupçonnes un comportement exponentiel, la première réaction est d'observer le comportement du logarithme de ta suite de valeurs (comme cela a été dit abondamment dans ce précédent fil). Avec plusieurs morceaux, en traçant le logarithme, tu dois pouvoir "voir" des portions de droites ! Avec un seul morceau, tu "verras" une seule série de points alignés ! Donc, ici, comme dans le fil précédent, tu traces la série des logarithmes de tes valeurs, et/ou tu fais une régression "linéaire" sur tes logs ! Le tracé lui-même n'est pas indispensable, mais il permet de décider de l'opportunité de la régression a priori et de valider cette régression a posteriori ! Je n'ai rien inventé, tout cela a déjà été dit dans le fil précédent !
-
Giansolo
- Membre Naturel
- Messages: 44
- Enregistré le: 02 Fév 2007, 14:38
-
 par Giansolo » 15 Mar 2007, 12:59
par Giansolo » 15 Mar 2007, 12:59
Merci pour ta réponse rapide, mais il y a un truc que je ne comprends pas : ok pour la régression linéaire sur les logs, mais comment introduire le fait qu'on puisse avoir une expo croissante, décroissante, concave ou convexe ? la modélisation par f(x) = a*exp(bx) +H ne modélise pas ce comportement si je ne m'abuse.
Quand à fitter un ensemble de points ou un sous ensemble pas de problèmes, comme tu dis : "qui peut le plus peut le moins".
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 15 Mar 2007, 13:20
par Quidam » 15 Mar 2007, 13:20
Giansolo a écrit:Merci pour ta réponse rapide, mais il y a un truc que je ne comprends pas : ok pour la régression linéaire sur les logs, mais comment introduire le fait qu'on puisse avoir une expo croissante, décroissante, concave ou convexe ? la modélisation par f(x) = a*exp(bx) +H ne modélise pas ce comportement si je ne m'abuse.
Quand à fitter un ensemble de points ou un sous ensemble pas de problèmes, comme tu dis : "qui peut le plus peut le moins".
La croissance ou la décroissance de ta courbe sera détectée par la régression ! Si tu trouves une droite d'équation y = ax +b qui approxime correctement tes points
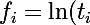)
(

), alors tu en déduiras immédatement en revenant aux

:
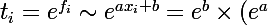^{x_i})
Si a>0 alors

: ton exponentielle est croissante.
Si a 0) ou qu'elle "descend" (a<0).
-
Giansolo
- Membre Naturel
- Messages: 44
- Enregistré le: 02 Fév 2007, 14:38
-
 par Giansolo » 15 Mar 2007, 14:51
par Giansolo » 15 Mar 2007, 14:51
Merci pour cette indication, j'imagine que le concavité ou la convexité (si ca se dit) suit la même loi.
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 15 Mar 2007, 16:26
par Quidam » 15 Mar 2007, 16:26
Giansolo a écrit:Merci pour cette indication, j'imagine que le concavité ou la convexité (si ca se dit) suit la même loi.
Non ! La concavité dépend du signe du coefficient : Si f(x)=a\times e^{bx}, la concavité est vers les y>0 si a>0, et le contraire si le contraire. Le signe de b change la croissance, pas la concavité !
Je me rends compte que je n'ai pas répondu à ton affirmation : "f(x) = a*exp(bx) +H ne modélise pas ce comportement si je ne m'abuse." Tu ne t'abuses pas ! Si H est différent de 0, en prenant le log de f tu ne trouveras pas une droite ! Ben tant pis !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
