voila j'ai un DM pour mercredi.Heureusement je le fais avec un ami donc les 2 questions plus dures sont deja faites.
Mais il reste encore 2 exos.
J'ai deja commence ms je bloque un tt petit peu enfin je ne suis pas sur:
EX1) soit le nb complexe z=e^ia - 1avec a dans ]o;2pi[.Trouver le module et un argument de z.
Pour le module, j'ai trouvé 2sin(a/2).
Mais pour l'argument je bloque: ca devrait etre du genre 2sin(a/2) e^i.teta
Mais je ne vois pas comment trouver teta,
puis le cercle trigonometrique est decalé dune unité vers la gauche, donc son centre est -1.Du coup en 0 un argument est tres petit et compris entre pi/2 et 3pi/2 ou est ce que je me tro,pe? si qq avait une petite idee quest ce qui est juste ce serait cool.
EX2)
Prerequis:
1.exp est une fonction derivable sur R
2.exp'=exp
3.exp(0)=1
4.exp(x).exp(-x)=1
5.exp(a+x)=exp(a) x exp(x)
En utilisant slt ces prerquis, montrer que:
a)pour tt reel, exp(x)>0
b)exp(x)+exp(-x)>ou= 2
En esperant une petite aide,
cordialement
T60 ;)
DM por Mercredi pas trop trop dur
10 messages
- Page 1 sur 1
salut,
pour l'exo 1 factorise exp(ia)-1 par exp(ia/2) et tu trouves direct module et argument (à retenir que ca aide bien de factoriser par l'angle moitié dans ce genre de cas : exp(ia)+exp(ib) il faudrait factoriser par exp(i(a+b)/2))
pour le 2b pose X=exp(x)et utilise 4) pour reconnaitre une identité remarquable
bonne chance :happy2:
pour l'exo 1 factorise exp(ia)-1 par exp(ia/2) et tu trouves direct module et argument (à retenir que ca aide bien de factoriser par l'angle moitié dans ce genre de cas : exp(ia)+exp(ib) il faudrait factoriser par exp(i(a+b)/2))
pour le 2b pose X=exp(x)et utilise 4) pour reconnaitre une identité remarquable
bonne chance :happy2:
ok ca me semble pas mal du tout, mais je veux etre sur de comprendre donc qq questions :
on a alors un module de 1 non? parce que si jai compris, |e(ia)|=1
pour l'argument on aurait donc a/2 ?
ainsi z=r e(ia) = 1e(i.a/2)=e(ia/2)
ou est ce qu'on ne pourrait ecrire pour factoriser : z= e(ia) (1-1/e(ia) )
=e(ia)-e(-ia)= 2isina dapres les formules d'Euler c-a-d: sina=[e(ia)-e(-ia)] /2i
d'ou module=2 et cosa+isina=isina, d'ou a=pi/2 , car cos(pi/2)=0 ??
je suis un peu confus.
pour le 2:
est ce que exp(-x)= 1/X
parce que je ne vois pas laquelle tu veux dire ?
on a alors un module de 1 non? parce que si jai compris, |e(ia)|=1
pour l'argument on aurait donc a/2 ?
ainsi z=r e(ia) = 1e(i.a/2)=e(ia/2)
ou est ce qu'on ne pourrait ecrire pour factoriser : z= e(ia) (1-1/e(ia) )
=e(ia)-e(-ia)= 2isina dapres les formules d'Euler c-a-d: sina=[e(ia)-e(-ia)] /2i
d'ou module=2 et cosa+isina=isina, d'ou a=pi/2 , car cos(pi/2)=0 ??
je suis un peu confus.
pour le 2:
est ce que exp(-x)= 1/X
parce que je ne vois pas laquelle tu veux dire ?
tu t'es un peu planté...
je te fais le premier, on a :
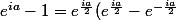)
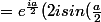)) (formule d'Euler pour le sinus)
(formule d'Euler pour le sinus)
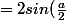e^{\frac{i(\pi+a)}{2}}) (i=e(iPi/2))
(i=e(iPi/2))
d'ou le module de) comme tu l'avais dit (positif car a est dans [0,2Pi] et l'argument : (Pi+a)/2
comme tu l'avais dit (positif car a est dans [0,2Pi] et l'argument : (Pi+a)/2
pour le 2b tu sais par 4) que exp(-x)=1/exp(x) et pas -exp(x) comme tu l'as écrit...
edit j'avais pas vu ton edit mais le 1 est toujours faux et le 2 c'est bon :happy2:
je te fais le premier, on a :
d'ou le module de
pour le 2b tu sais par 4) que exp(-x)=1/exp(x) et pas -exp(x) comme tu l'as écrit...
edit j'avais pas vu ton edit mais le 1 est toujours faux et le 2 c'est bon :happy2:
OK j'ai pas vu quelle identité remarquable tu voulais dire, je l'ai résolu (j'espere correctement) avec 2 autres méthodes, en utilisant les caracteristiques d'une parabole entre autre.
Si tu pouvais m'expliquer q mm comment tu aurais fait ca serait cool :)
Merci encore pour ton aide precieuse!! :happy2:
Si tu pouvais m'expliquer q mm comment tu aurais fait ca serait cool :)
Merci encore pour ton aide precieuse!! :happy2:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
