Petit problème à résoudre
21 messages
- Page 1 sur 2 - 1, 2
Petit problème à résoudre
Bonjour,
J'ai un problème de réseau à résoudre, mais l'énoncé s'apparente plus à quelque chose de méthématiques, donc j'espère pouvoir trouver ici réponse à mon problème !
Voici l'énoncé :
Un groupe de (2^n);) 1 routeurs sont interconnectés selon une arborescence binaire centralisée comportant un routeur par nud. Le routeur i communique avec le routeur j en envoyant un message à la racine qui le transmet à ce dernier. Déduisez une expression aproximative du nombre moyen de bonds par messages pour une valeur n élevée, en partant du principe que toutes les paires de routeurs sont semblables.
Voilà.
Merci d'avance. Pour toute question, vous pouvez m'envoyer un message privé ;)
Bonne journée à tous.
J'ai un problème de réseau à résoudre, mais l'énoncé s'apparente plus à quelque chose de méthématiques, donc j'espère pouvoir trouver ici réponse à mon problème !
Voici l'énoncé :
Un groupe de (2^n);) 1 routeurs sont interconnectés selon une arborescence binaire centralisée comportant un routeur par nud. Le routeur i communique avec le routeur j en envoyant un message à la racine qui le transmet à ce dernier. Déduisez une expression aproximative du nombre moyen de bonds par messages pour une valeur n élevée, en partant du principe que toutes les paires de routeurs sont semblables.
Voilà.
Merci d'avance. Pour toute question, vous pouvez m'envoyer un message privé ;)
Bonne journée à tous.
Voilà. Et donc en partant d'un routeur quelconque i, on veut envoyer un message à un autre routeur quelconque j. Et donc on veut savoir combien de bonds on doit faire, en partant de i, sachant qu'on doit passer par la racine (cad le routeur 1), avant de rejoindre le routeur j. Un bonds ce doit être le fait de passer d'un routeur à un autre.
Et c'est faire ce calcul qui me pose problème, je ne vois pas trop comment faire :(
Et c'est faire ce calcul qui me pose problème, je ne vois pas trop comment faire :(
Comme tous les messages passent par la racine, au lieu de considérer un arbre binaire, on va considérer un martinet (un fouet pour enfants). Soit 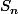 le martinet dont les lanières sont de longueur
le martinet dont les lanières sont de longueur 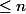 . Il est parfaitement décrit:
. Il est parfaitement décrit:
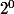 lanière de longueur 0,
lanière de longueur 0, 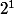 lanières de longueur 1,...,
lanières de longueur 1,..., lanières de longueur n.
lanières de longueur n.
Il comporte routeurs.
routeurs.
il comporte ") "=
"=(2^{n}-1)) paires de routeurs.
paires de routeurs.
On suppose qu'un message transite entre chaque paire et on appelle
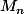 la somme des distances parcourues.
la somme des distances parcourues.
nous cherchons une formule de récurrence entre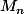 et
et 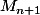 .
.
Au coup n+1, on rajoute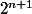 routeurs. Au rang n+1,
routeurs. Au rang n+1,
il y a :
a) les paires dont les deux routeurs sont à une distance n+1
b)les paires dont les deux routeurs sont à une distance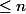
c)les paires dont un routeur est à une distance n+1 et l'autre routeur
à distance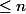
nous évaluons les chemins parcourus par les messages pour les cas (a),(b) et (c).
Il comporte
il comporte "
On suppose qu'un message transite entre chaque paire et on appelle
nous cherchons une formule de récurrence entre
Au coup n+1, on rajoute
il y a :
a) les paires dont les deux routeurs sont à une distance n+1
b)les paires dont les deux routeurs sont à une distance
c)les paires dont un routeur est à une distance n+1 et l'autre routeur
à distance
nous évaluons les chemins parcourus par les messages pour les cas (a),(b) et (c).
cas (a):
chaque message d'une paire fait un chemin de longueur 2(n+1).
Il y a "2 parmi (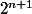 )"=
)"=) paires.
paires.
d'où le cas (a) contribue pour une distance totale parcourue de :
2^{n+1}(2^{n+1}-1)) .
.
cas(b):
les messages parcourt une distance totale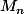 par hypothèse de récurrence.
par hypothèse de récurrence.
cas (c):
il y a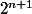 routeurs à distance n+1.
routeurs à distance n+1.
Chaque routeur se paire avec les routeurs du martinet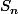 :
:
on obtient un cumul de distances pour un routeur à distance n+1:
+2^1 (n+2)+2^2 (n+3)+...+(n+n+1) 2^{n})
soit pour un routeur à distance n+1:
+(1+2.2^1 + 3.2^2 + ...+(n+1).2^{n}))
le 2ème terme de la somme s'évalue en dérivant la fonction
chaque message d'une paire fait un chemin de longueur 2(n+1).
Il y a "2 parmi (
d'où le cas (a) contribue pour une distance totale parcourue de :
cas(b):
les messages parcourt une distance totale
cas (c):
il y a
Chaque routeur se paire avec les routeurs du martinet
on obtient un cumul de distances pour un routeur à distance n+1:
soit pour un routeur à distance n+1:
le 2ème terme de la somme s'évalue en dérivant la fonction
Ouaaa la je suis complètement perdu lol. Avec un arbre je comprenais la chose.
J'ai fais ce dessin pour mieux se rendre compte :

Et donc le truc c'est de passer de I à J, en passant par le n°1 obligatoirement (même dans le cas ou I et J sont du même coté). Et donc combien de sauts d'un noeud à l'autre on doit faire ?
Car la avec le martinet, déjà on est à (2^n+1) -1 au lieu de (2^n) - 1 routeurs, et je n'arrive pas du tout à me représenté les noeuds !
J'ai fais ce dessin pour mieux se rendre compte :

Et donc le truc c'est de passer de I à J, en passant par le n°1 obligatoirement (même dans le cas ou I et J sont du même coté). Et donc combien de sauts d'un noeud à l'autre on doit faire ?
Car la avec le martinet, déjà on est à (2^n+1) -1 au lieu de (2^n) - 1 routeurs, et je n'arrive pas du tout à me représenté les noeuds !
j'interromp mon calcul pour expliquer comment on passe d'un arbre à un martinet:
si un message transite d'un routeur à l'autre, il dédouble en quelque sorte le
chemin parcouru. on peut alors considérer que chaque routeur est au bout d'une corde, ce qui donne un martinet. De plus, j'ai pris pour racine la profondeur zéro et pas la profondeur 1. Quand on passe de la profondeur n à n+1, on rajoute au martinet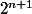 lanières de longeur n+1.
lanières de longeur n+1.
si un message transite d'un routeur à l'autre, il dédouble en quelque sorte le
chemin parcouru. on peut alors considérer que chaque routeur est au bout d'une corde, ce qui donne un martinet. De plus, j'ai pris pour racine la profondeur zéro et pas la profondeur 1. Quand on passe de la profondeur n à n+1, on rajoute au martinet
Bin ouai mais dans ce cas la ca voudrait dire que pour chaque bonds on doit passer par la racine, hors on ne passe par la racine qu'une seule fois !
Si tu veux, I envoie un message destiné à J. Pour cela, il envoie un message au routeur d'en dessous de lui, qui lui même envoie ce msg encore en dessous, etc, jusqu'à envoyer le msg à la racine. Et là, même procédé mais dans l'autre sens : la racine envoie au routeur juste au dessus, ce dernier renvoie encore au dessus, jusqu'à arriver à J. Et on compte le nombre d'envois.
Si tu veux, I envoie un message destiné à J. Pour cela, il envoie un message au routeur d'en dessous de lui, qui lui même envoie ce msg encore en dessous, etc, jusqu'à envoyer le msg à la racine. Et là, même procédé mais dans l'autre sens : la racine envoie au routeur juste au dessus, ce dernier renvoie encore au dessus, jusqu'à arriver à J. Et on compte le nombre d'envois.
En m'aidant de certaines de tes lignes pour piger la chose, j'ai trouvé que en fait, sur une branche au maximum on avant n-1 bonds. Donc admettons que les 2 routeurs soit chacun à un bout, ca ferais 2n-2 bonds pour faire le trajet entre les 2. Le min étant 2 bonds si chaque routeur est juste à coté de la racine.
Le nombre moyen pour arriver à la racine devient donc:
(1+...+n-1) / (n-1)
Pareil pour le récepteur. Puis on additionne les 2.
Je me trompe qque part ou pas ?
Car en fait le résultat doit être simple, c'est un prof de réseau qui a donné le calcul, pas un prof de math :D
Le nombre moyen pour arriver à la racine devient donc:
(1+...+n-1) / (n-1)
Pareil pour le récepteur. Puis on additionne les 2.
Je me trompe qque part ou pas ?
Car en fait le résultat doit être simple, c'est un prof de réseau qui a donné le calcul, pas un prof de math :D
j'ai donc la formule de récurrence:
+2^{n}((n-1)2^{n+1}-(n-2)))
la formule est vraie encore pour n=2 (je le vérifie à la main)
et donne pour les premiers termes:
 et
et  (martinet de longueur 0 et de longueur
(martinet de longueur 0 et de longueur  1)
1)
d'où en sommant:
+2^{k}((k-1)2^{k+1}-(k-2)))
en arrangeant cette somme:
4^{k}-(k-1).2^{k+1})
une fois cette somme calculée, le nombre moyen de bonds par message
est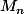 divisé par le nombre de paires du martinet de rang n ,nombre de paires que j'ai calculé dans un message précédent.
divisé par le nombre de paires du martinet de rang n ,nombre de paires que j'ai calculé dans un message précédent.
je vais diner...
la formule est vraie encore pour n=2 (je le vérifie à la main)
et donne pour les premiers termes:
d'où en sommant:
en arrangeant cette somme:
une fois cette somme calculée, le nombre moyen de bonds par message
est
je vais diner...
tous calculs faits:
4^{n}-4(n-2)2^{n}-4)
le nombre moyen de bonds au rang n est donc:
(2^{n}-1)})
en divisant par le nombre de paires du martinet de longueur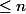
le nb moyens de bonds est donc exactement:
4^{n}-4(n-2)2^{n}-4}{2.4^n-3.2^{n}+1})
pour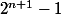 routeurs.
routeurs.
donc de l'ordre de:
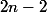
la formule est juste. Pour un martinet de lanières de longueur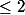 ,
,
i.e, un arbre de 7 routeurs, elle donne un nombre moyen de bonds de
2,86.
le nombre moyen de bonds au rang n est donc:
en divisant par le nombre de paires du martinet de longueur
le nb moyens de bonds est donc exactement:
pour
donc de l'ordre de:
la formule est juste. Pour un martinet de lanières de longueur
i.e, un arbre de 7 routeurs, elle donne un nombre moyen de bonds de
2,86.
$h1n a écrit:Bin ouai mais dans ce cas la ca voudrait dire que pour chaque bonds on doit passer par la racine
non, ça ne veut pas dire ça. Je suis déçu que tu ne cherches pas à comprendre mon histoire de martinets.De toute façon, le message ne remonte jamais à la racine de l'arbre mais redescend dès que possible, ce qui est matière à un autre dénombrement.
O non ne prend pas mal la manière dont je répond, ce n'est pas que je ne cherche pas à comprendre, au contraire ! Mais c'est que par un dessin si tu veux je n'arrive pas à me le représenter, et comme je ne suis pas doué en math, je peine à me représenté juste par des opérations :(
Mais je crois avoir compris quelques trucs quand même, je vais tout reprendre tête reposée pour tout bien comprendre.
Mais si j'ai bien compris, ceci est valable (2^n+1) -1 routeurs.
Donc pour (2^n) - 1 routeurs, il faut oter un terme à la somme, ca ferait 2n-4 non ?
Mais je crois avoir compris quelques trucs quand même, je vais tout reprendre tête reposée pour tout bien comprendre.
Mais si j'ai bien compris, ceci est valable (2^n+1) -1 routeurs.
Donc pour (2^n) - 1 routeurs, il faut oter un terme à la somme, ca ferait 2n-4 non ?
oui, c celà. Il doit effectivement avoir un raisonnement simple (on dit "heuristique") pour trouver 2n-4 rapidement.
bon allez finalement méthode heuristique:
il y a 2^0 routeur à une distance 0 de la racine
il y a 2^1 routeurs à une distance 1 de la racine
...
il y a 2^n routeur à une distance n de la racine
un trajet d(i,j)=d(0,i)+d(0,j) comme tu l'as dit:
d(0,i) vaut en moyenne
reste plus qu'à calculer le numérateur grace à la dérivation de :
bon allez finalement méthode heuristique:
il y a 2^0 routeur à une distance 0 de la racine
il y a 2^1 routeurs à une distance 1 de la racine
...
il y a 2^n routeur à une distance n de la racine
un trajet d(i,j)=d(0,i)+d(0,j) comme tu l'as dit:
d(0,i) vaut en moyenne
reste plus qu'à calculer le numérateur grace à la dérivation de :
$h1n,
je remonte le fil car je m'intéresse au même problème optimisé:
Un groupe de (2^n);) 1 routeurs sont interconnectés selon une arborescence binaire centralisée comportant un routeur par nud. Déduisez une expression approximative du nombre moyen de bonds par messages pour une valeur n élevée,
Le routeur i communique avec le routeur j en envoyant un message PAR LE PLUS COURT CHEMIN.
Je vais exploiter le caractère binaire de l'arbre.
je remonte le fil car je m'intéresse au même problème optimisé:
Un groupe de (2^n);) 1 routeurs sont interconnectés selon une arborescence binaire centralisée comportant un routeur par nud. Déduisez une expression approximative du nombre moyen de bonds par messages pour une valeur n élevée,
Le routeur i communique avec le routeur j en envoyant un message PAR LE PLUS COURT CHEMIN.
Je vais exploiter le caractère binaire de l'arbre.
Nous gardons les notations suivantes:
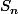 désigne l'arbre à
désigne l'arbre à 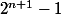 routeurs comprenant:
routeurs comprenant:
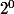 routeur sur la racine
routeur sur la racine
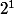 routeurs à la profondeur 1
routeurs à la profondeur 1
...
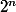 routeurs à la profondeur n.
routeurs à la profondeur n.
Cette fois, on suppose que les messages transitent d'un routeur à l'autre
par le plus court chemin. On va calculer la distance moyenne entre deux routeurs en moyennant cette distance sur toutes les paires de routeurs de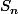 . On calcule la somme des distances entre deux routeurs, sommation effectuée sur l'ensemble des paires de
. On calcule la somme des distances entre deux routeurs, sommation effectuée sur l'ensemble des paires de 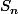 , notons cette somme
, notons cette somme 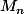 .
.
on a :

On calcule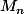 par récurrence:
par récurrence:
Soit la racine de l'arbre
la racine de l'arbre 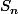 et
et  et
et 
les routeurs de profondeur 1 qui sont les racines de deux arbres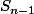 .
.
On partitionne l'ensemble des paires de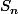 en trois classes:
en trois classes:
(a) 2 fois les paires dont les deux élements appartiennent à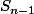
car il y a deux sous arbres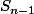
(b) 2 fois: les paires dont un élément est la racine de
de 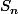 et l'autre élément dans
et l'autre élément dans 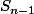
(c) les paires dont un élement est dans un sous arbre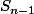 et l'autre élément dans le sous-arbre symétrique de
et l'autre élément dans le sous-arbre symétrique de 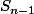
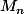 est donc la somme de:
est donc la somme de:
(a) les distances cumulées sur les paires du cas (a) soit 2 .
.
(b) les distances cumulées sur les paires du cas (b) soit:
)
(c) les distances cumulées sur les paires du cas (c):
à cause de la symétrie, il s'agit des distances de COUPLES de routeurs
dont les éléments appartiennent à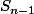 , distances évaluées en repassant par la racine
, distances évaluées en repassant par la racine 
On obtient la formule de récurrence:
4^{n} \qquad)
)
En sommant les égalités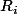 pour i de 2 à n avec un coefficient
pour i de 2 à n avec un coefficient
 il vient:
il vient:
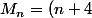2^{n+1}+(n-2)4^{n+1})
d'où le nombre moyen de rebonds pour(2^{n}-1)) paires:
paires:
2^{n+1}+(n-2)4^{n+1}}{2.4^{n}-3.2^{n}+1})
Quand n devient grand, le nombres moyens de rebonds par message
est) alors que si les messages transitent par la racine,
alors que si les messages transitent par la racine,
on avait trouvé :)
...
Cette fois, on suppose que les messages transitent d'un routeur à l'autre
par le plus court chemin. On va calculer la distance moyenne entre deux routeurs en moyennant cette distance sur toutes les paires de routeurs de
on a :
On calcule
Soit
les routeurs de profondeur 1 qui sont les racines de deux arbres
On partitionne l'ensemble des paires de
(a) 2 fois les paires dont les deux élements appartiennent à
car il y a deux sous arbres
(b) 2 fois: les paires dont un élément est la racine
(c) les paires dont un élement est dans un sous arbre
(a) les distances cumulées sur les paires du cas (a) soit 2
(b) les distances cumulées sur les paires du cas (b) soit:
(c) les distances cumulées sur les paires du cas (c):
à cause de la symétrie, il s'agit des distances de COUPLES de routeurs
dont les éléments appartiennent à
On obtient la formule de récurrence:
En sommant les égalités
d'où le nombre moyen de rebonds pour
Quand n devient grand, le nombres moyens de rebonds par message
est
on avait trouvé :
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
