Deux questions de probabilité

[Adrom]

Bonjour,

J'utilise rarement des forums pour poser mes questions et j'arrive d'habitude à m'entendre avec mon ami google.
Mais il faut croire que cette fois il n'a pas de réponse, ou du moins je n'arrive pas à bien poser ma question...

Je vous remercie donc par avance si vous pouvez m'éclairer.

Question N°1 :

Un jet de (peu importe) à 10% de réussite.
On effectue 5 jets.
Combien à t'on de chance d'obtenir au moins 1 réussite ?

J'aimerai arriver à une formule avec comme inconnus :
Le % de réussite du jet.
Le nombre de jets effectués.


Question N°2 :
C'est plutôt la suite de la question enfaite mais en plus élaboré.

On doit effectuer un jet (A) à 10% de réussite.
Une fois qu'une réussite à été obtenu on doit effectuer un jet (B) à 2% de réussite.
Une fois qu'une réussite à été obtenu on doit effectuer un jet (C) à 15% de réussite.
On effectue 50 jets (tout confondu).
Combien à t'on de chance d'obtenir les 3 réussites ?

J'aimerai arriver à une formule avec comme inconnus :
Le % de réussite du jet (A).
Le % de réussite du jet (B).
Le % de réussite du jet (C).
Le nombre de jets effectués.

Bonne soirée,
Emeric,

[Ben314]

Salut,
La question 1) est "plus que classique" : si tu fait un certain nombre fois une même expérience aléatoire ayant une probabilité de réussite alors alors la proba. d'avoir un échec est 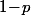et, si les résultat des différentes tentatives sont indépendants, la proba. de n'avoir que des échecs est donc celle d'avoir au moins une réussite est .

Pour la question 2), c'est pas clair : une fois que tu as ta première réussite de l’événement A et que tu tente B, si tu rate, tu retente B ou tu recommence au début avec A ? (idem évidement avec B et C)

[Adrom]

Merci pour cette réponse rapide.
"plus que classique", je n'en doutais pas, mais mes cours de proba sont relativement loin

Pour la question 2, :
Une fois le test A réussi. c'est validé, pas besoin de recommencer.
donc si tu rate B tu retente B ensuite.
De même pour C.

[Ben314]

La proba qu'il faille exactement tentatives pour valider A est où est la proba de réussite de A.
Idem pour B et C avec des proba respectives de et .
Donc si au total tu as le droit à tentatives, la proba d'y arriver, c'est la somme des prise sur tout les triplets d'entiers naturels non nuls tels que .
Et ça se simplifie (je le ferais lorsque j'aurais du temps).

[lyceen95]

Question 1
Quand il y a 'au moins' dans une question, c'est souvent plus efficace de chercher la probabilité complémentaire.
Quelle est la probabilité d'avoir au moins un succès, cherchons la probabilité d'avoir uniquement des échecs.
Et ça, c'est facile : 0.9^5
Donc la proba d'avoir au moins un succès, c'est 1 -0.9^5=0.41

Question 2
C'est beaucoup beaucoup plus compliqué. Pour avoir un résultat précis, je ne vois qu'un recensement 'exhaustif' ou assimilé.
Mais de toutes façons, la probabilité finale est assez faible. Admettons qu'on soit chanceux, t au premier lancer, on a un succès ( proba = 1/10).
Ensuite, on a 48 lancers pour tenter d'obtenir un succès avec le 2ème objet (proba d'échouer 48 fois = 37.9%), c'est beaucoup et ensuite, il faut réussir l'épreuve C, en 1 lancer.

Pour que ce soit plus facile à 'modéliser', changeons l'ordre des dés. D'abord le plus facile, puis le moyen, puis le plus difficile.
Avec le dé à 85%, il faut en gros 4 ou 5 lancers en moyenne pour obtenir un premier succès.
Avec le dé à 80%, il faut en gros 5 ou 6 lancers en moyenne pour avoir un premier succès.
Il nous reste donc environ 40 lancers avec l'autre dé. Et la probabilité d'avoir 40 échecs est d'environ 45%.
Donc au final, on a une probabilité d'environ 55% de réussir. Calcul assez approximatif.

[Ben314]

Pour la question 2), si je ne me suis pas trop gouré, ça donne ça :

(à interpréter en terme de limite lorsque deux des probas. sont les mêmes)

[lyceen95]

C'est assez surprenant d'avoir des , surtout au dénominateur, mais les résultats numériques obtenus avec ta formule semblent tout à fait plausibles !

[Adrom]

Merci pour toutes vos réponses.

Le but est d'utiliser ces formules dans du JavaScript.

je ne vois qu'un recensement 'exhaustif' ou assimilé.

Donc en soit un "recensement exhaustif" est possible, mais les formules de Ben seront plus optimisé.

Je vais en profiter pour faire un petite simulation (de milliers de tirage) pour vérifier que tout fonctionne bien.

(à interpréter en terme de limite lorsque deux des probas. sont les mêmes)

Je devrait pouvoir faire des conditions pour utiliser la formule différemment dans les cas d'exceptions.
J'ai aussi un cas (où je n'ai pas poser la question au début) avec seulement 2 test au lieux de 3 et je doit aussi trouver le nombre de jet "N" pour une proba de 50%.

Mais avec vos réponse je vais pouvoir avancer.
Je paramètre tout ça et je vous tiens au courant de si tout fonctionne bien.

[Adrom]

Me revoilà,

Donc ça fonctionne et ça ne fonctionne pas.
Ce que je vous ai demandé fonctionne, mais en voyant ces résultats, je comprend que j'ai mal réalisé ma demande.

1] J'ai donc fait une simulation de mon problème comparé à la formule de ben. Quelque résultat qui parle d'eux même ci-dessous :

Test N°1 :
Paramètre : pA = 10%, pB = 5%, pC = 20%, N (tentative) = 12
Résultat de la simulation avec une profondeur de 20000 expériences : 9.98%
Résultat via la formule : 10.1%

Test N°2 :
Paramètre : pA = 1%, pB = 15%, pC = 0.5%, N (tentative) = 120
Résultat de la simulation avec une profondeur de 20000 expériences : 18.6%
Résultat via la formule : 18.7%

Test N°3 :
Paramètre : pA = 1%, pB = 15%, pC = 1%, N (tentative) = 300
Résultat de la simulation avec une profondeur de 20000 expériences : 79.22%
Résultat via la formule : 79.2%
(j'ai "résolu" le problème des probabilité égale avec une technique de roublard :
pA = 1% + 0.0000000001 et pC = 1% + 0.0000000002 ... )

donc ici tout fonctionne bien.

2] Il y a en faite une légère subtilité dans les trois test à réalisé mais qui bouge probablement toute la formule voir la simplifie ? :
La première tentative de chaque test est "gratuite" ou dit différemment la réussite d'un test ne consomme pas de tentative.

J'ai donc ajusté ma simulation tout en conservant la même formule et j'obtiens ces résultats :

Test N°1 :
Paramètre : pA = 10%, pB = 5%, pC = 20%, N (tentative) = 12
Résultat de la simulation avec une profondeur de 20000 expériences : 14.04%
Résultat via la formule : 10.1%

Test N°2 :
Paramètre : pA = 1%, pB = 15%, pC = 0.5%, N (tentative) = 120
Résultat de la simulation avec une profondeur de 20000 expériences : 19.28%
Résultat via la formule : 18.7%

Test N°3 :
Paramètre : pA = 1%, pB = 15%, pC = 1%, N (tentative) = 300
Résultat de la simulation avec une profondeur de 20000 expériences : 79.15%
Résultat via la formule : 79.2%

Test N°4 :
Paramètre : pA = 20%, pB = 15%, pC = 30%, N (tentative) = 5
Résultat de la simulation avec une profondeur de 20000 expériences : 15.91%
Résultat via la formule : 6.33%

On peut voir que l'impact deviens important avec un nombre de tentative réduite, logique.
Mais ce cas de figure devrait arriver régulièrement lors de l'utilisation de mon petit programme, ce qui est un peu embêtant.

3] Je doit aussi donner le nombre de tentative nécessaire pour avoir une réussite de 50% pour chaque test et pour le global des 3 tests.

J'ai réussi à retourner la formule pour un test (enfin je croit) :

---->

Par-contre retourner l'autre ..

heu...

4] J'aurais un aussi un cas avec 2 test au lieux de 3. Je ne sais pas si la formule sera simplifiable aisément ?


J'abuse clairement de votre temps.
Mais il est si facile de demander...

Je vous remercie en tout cas pour vos précédentes réponse.

[Ben314]

C'est assez surprenant d'avoir des , surtout au dénominateur, mais les résultats numériques obtenus avec ta formule semblent tout à fait plausibles !

Ca provient du fait que la formule que tu utilise en cascade pour les calculs est celle des suites géométriques :

qui n'est évidement valable que pour (sinon la somme fait bêtement ).
Et là, tu doit en particulier utiliser la formule avec et donc le résultat n'est pas valable lorsque mais "presque" valable dans le sens qu'il suffit de regarder ce qu'il se passe lorsque tend vers .

[lyceen95]

Si la 1ère tentative pour chaque nouveau 'dé' est gratuite, je pense que tu peux toujours utiliser la formule de Ben314, mais en ajoutant 3 au nombre total de lancers.

Du coup pour le dernier test, en remplaçant N=5 par N=8, la formule de Ben314 donne 21.4%
Ca ne colle toujours pas avec tes simulations.
A priori, Ce n'est pas 3 qu'il faut ajouter, mais 2. Peut-être que le premier lancer du 1er dé n'est pas gratuit dans tes tests ?

En ajoutant 2 à N, ça a l'air de coller pour les différents exemples.

[Ben314]

(j'ai "résolu" le problème des probabilité égale avec une technique de roublard :
pA = 1% + 0.0000000001 et pC = 1% + 0.0000000002 ... )

C'est effectivement la façon la plus simple de procéder et mathématiquement parlant, c'est parfaitement valable vu que, malgré les apparences de la formule, on a bien sûr affaire à une fonction dépendant continuement des probas .

Pour l'histoire des "réussites gratuites", à priori, je pense comme Lycéen, à savoir qu'il doit suffire d'augmenter N de 3 (augmenter de 2 me semble assez surprenant : vérifie bien que ton programme est tapé correctement).

Sinon, avec que deux trucs à valider, la formule (avec le même contexte) c'est

[Adrom]

J'ai essayé pas mal d'itération et effectivement la formule avec n+2 colle parfaitement à mon programme.
J'ai retourné mon code dans tout les sens et je vois pas ce qui pourrais clocher.
Ca va me faire un sujet de réflexion ce soir au lieux de compter les moutons.

Toujours est-il que la formule soit avec n+2 ou n+3 elle fonctionnera, donc merci pour ça.

merci

Bonne soirée,