Exercice suite maths expertes TS

[FernandAimeLesMaths]

Bonjour, je suis bloqué sur un exercice de maths expertes :

"On considère la suite des enters 31, 331, 3331, ... et on note Un l'entier de la suite dont l'écriture comporte n fois le chiffre 3.

1. Rappeler comment démontrer que les sept premiers termes de la suite (Un) sont premiers.

2. a) Sans justifier, donner la valeur de la différence Un+1 - Un pour tout entier n non nul.
b) En déduire (à l'aide d'un raisonnement par récurrence par exemple) que : 3Un= ((10^n+1) -7) pour tout n appartenant à N*
3. Cas ou n = 8.
a) Vérifier que 10^2 congru -2 [17]
En déduire le reste de la division euclidienne de 10^9 par 17.
b) Démontrer que Un est divisible par 17.
c) Justifier que : 10^16 congru 1 [17]
En déduire que pour tout entier naturel k, U (indice 16k+ 8) est divisible par 17.
4. Cas où n = 11
a) Vérifier que 10^2 congru 5 [19]
En déduire le reste de la division euclidienne de 10^12 par 19,
b) Démontrer que Un est divisible par 19.
c) Justifier que 10^18 congru 1|19].
En déduire que pour tout entier naturel k, U(indice 18k+11) est divisible par 19."

Je pense avoir réussi pour les questions 3 et 4 mais je ne vois pas pour leur petit c.

Merci d'avance.

[lyceen95]

Pour la question 3c)

On sait que
Donc puis pui

[FernandAimeLesMaths]

Bonjour,

D'accord, donc pour la 3)c) :
10^4 ≡ (-2)^2 ≡ 4 [17]
10^8 ≡ 4^2 ≡ 16 [17]
10^16 ≡ 16^2 ≡ 256 ≡ 1 [17]

Je ne vois pas comment justifier que U(indice 16k+ 8) est divisible par 17 ensuite ?

[lyceen95]

A la question 1b, on a montré que pour tout entier

Et donc pour tout entier .

, on n'a pas encore de résultat qui parle de ce nombre, mais on a des résultats sur et d'autres résultats sur .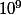
Il ne reste qu'à assembler le puzzle.

[FernandAimeLesMaths]

Ah d'accord, merci beaucoup !
Très bien, alors du coup j'ai maintenant réussi à répondre aux questions 3 et 4, mais il me reste encore les questions 1 et 2.

Pour la 1, faut-il trouver l'expression de Un pour répondre ou utiliser un théorème en particulier ?
Car de toute manière il la faudra pour la 2, donc... ?

En tous cas, tu m'as déjà bien aidé, merci.

[lyceen95]

La 1 : J'ai une vague idée, mais je ne suis pas sûr que ce soit la réponse attendue par ton prof.
Normalement, il attend que vous répétiez un truc qu'il a dit en cours, hier ou avant-hier.

La 2a est hyper-facile
La 2b est un peu plus longue, mais facile aussi.

Tu n'as pas besoin de l'expression de pour aucune de ces questions : on te guide pas à pas, on te donne toutes les indications. Si tu avais besoin de l'expression de , l'énoncé dirait de calculer l'expression de .