Condition nécessaire pour un extremum local
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 02 Avr 2021, 11:01
par Frandom94 » 02 Avr 2021, 11:01
Bonjour à toutes et à tous,
Dans la propriété suivante : soit f une fonction définie sur l’intervalle ouvert I de R. Si f admet un extremum en a de I alors f'(a) =0, je me demande pourquoi on exige de I qu'il soit ouvert.
Quelqu'un pourrait-il m'aider à lever le doute ?
Bonne journée à vous !

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 02 Avr 2021, 11:05
par GaBuZoMeu » 02 Avr 2021, 11:05
Bonjour,
Regarde ce qui se passe pour la fonction
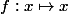
définie sur l'intervalle fermé [0,1].
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 02 Avr 2021, 12:26
par Frandom94 » 02 Avr 2021, 12:26
Ok c'est clair pour cet exemple. Pour être sûr de comprendre, cela veut dire que sur le même intervalle ouvert, f n'admet pas d'extrémum ?
J'ai toujours un peu de mal à voir ce qu'il se passe dans le cas général.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 02 Avr 2021, 12:44
par hdci » 02 Avr 2021, 12:44
Bonjour,
Quelle est la définition d'un maximum ? C'est une valeur

telle qu'il existe

vérifiant
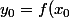)
, et telle que pour tout x de l'ensemble de définition,
\geq y_0)
Même chose pour le minimum.
Le point crucial est "'il existe

vérifiant
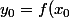)
". Ainsi, la fonction
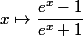
est bornée, strictement croissante sur IR mais n'a ni maximum ni minimum.
Sachant cela, y a-t-il un maximum à la fonction
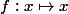
définie sur
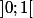
?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 02 Avr 2021, 14:05
par catamat » 02 Avr 2021, 14:05
Bonjour,
C'est plutôt bien expliqué sur cette page :
https://fr.wikiversity.org/wiki/Fonctio ... emum_local(désolé le lien passe mal cliquez sur celui qui apparait dans la page wiki : derivee extremum local)
soit f une fonction définie sur l’intervalle ouvert I de R. Si f admet un extremum en a de I alors f'(a) =0
Vous avez oublié de dire que f est dérivable sur I
-
mathelot
 par mathelot » 02 Avr 2021, 16:57
par mathelot » 02 Avr 2021, 16:57
hdci a écrit:Quelle est la définition d'un maximum ? C'est une valeur

telle qu'il existe

vérifiant
)
, et telle que pour tout x de l'ensemble de définition,
\geq y_0)
Sachant cela, y a-t-il un maximum à la fonction
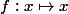
définie sur
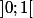
?
bonsoir,
il y a une erreur dans la définition
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 02 Avr 2021, 18:18
par hdci » 02 Avr 2021, 18:18
Exact, deux erreurs en fait : j'ai écrit \geq au lieu de \leq en latex, et j'ai fait court en prenant la définition du maximum global et non local.
Donc pour un maximum local, la définition à retenir est : il existe un intervalle ouvert contenant

tel que pour tout x appartenant à l'intervalle INTER l'ensemble de définition, on ait
\leq y_0)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
mathelot
 par mathelot » 02 Avr 2021, 18:41
par mathelot » 02 Avr 2021, 18:41
On peut supposer, pour simplifier , que la fonction f est définie sur un intervalle de R ouvert non vide
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 02 Avr 2021, 19:10
par hdci » 02 Avr 2021, 19:10
Mais la question initiale était "pourquoi fallait-il que l'intervalle soit ouvert" (car u maximum local peut être atteint sur un intervalle fermé, sans que la dérivée ne s'y annule) ; il faut donc bien définir le maximum en prenant en compte un ensemble pas forcément ouvert.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
mathelot
 par mathelot » 02 Avr 2021, 20:01
par mathelot » 02 Avr 2021, 20:01
La fonction f admet un maximum local en x0 à la condition que f soit définie sur un voisinage de x0
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 02 Avr 2021, 20:52
par Frandom94 » 02 Avr 2021, 20:52
hdci a écrit:Bonjour,
Quelle est la définition d'un maximum ? C'est une valeur

telle qu'il existe

vérifiant
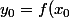)
, et telle que pour tout x de l'ensemble de définition,
\geq y_0)
Même chose pour le minimum.
Le point crucial est "'il existe

vérifiant
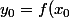)
". Ainsi, la fonction
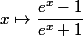
est bornée, strictement croissante sur IR mais n'a ni maximum ni minimum.
Sachant cela, y a-t-il un maximum à la fonction
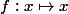
définie sur
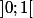
?
D'accord, j'avais senti l'idée mais je n'étais pas bien sûr de mon coup ! On peut trouver des majorants, mais aucun d'eux n'est jamais atteint quand l'intervalle est ouvert. Merci beaucoup à toi

-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 02 Avr 2021, 20:53
par Frandom94 » 02 Avr 2021, 20:53
Merci à tous pour vos réponses ! ^^
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 02 Avr 2021, 21:02
par hdci » 02 Avr 2021, 21:02
mathelot a écrit:La fonction f admet un maximum local en x0 à la condition que f soit définie sur un voisinage de x0
La fonction
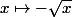
admet un maximum (global en outre) en 0, mais elle n'est pas définie au voisinage de 0 dans

, uniquement au voisinage de 0 dans
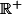
, d'où l'intersection de l'intervalle ouvert contenant 0 et intersecté avec l'ensemble de définition.
Si on considère la topologie induite sur l'ensemble de définition, toute fonction est définie au voisinage de tous les points de son ensemble de définition.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
