Condition nécessaire et suffisante

par **ice456** » 01 Déc 2007, 16:13

Bonjour à tous,

il nous est demandé de donner une condition nécessaire et suffisante sur f* (en fonction de

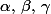
et k) pour que f(x) = f* admette au moins une solution t

0 avec

.

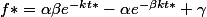
On a donc que f(x) = f*

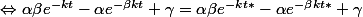
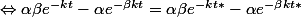
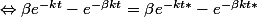
donc pas de condition sur

mais je ne vois pas comment continuer pour déterminer des condition sur

et sur k.

Merci pour votre aide et vos pistes.

par **yos** » 01 Déc 2007, 16:18

Bonjour.
C'est quoi l'étoile? La conjugaison complexe?

par **ice456** » 01 Déc 2007, 16:22

Désolé j'ai mal introduit le problème.

On a une équation générale qui nous permet de donner la température d'un corps à un temps t précis : f(t) =

+

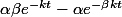
Et f* est la température du corps à un moment t*

J'espère avoir été assez clair sinon n'hésite pas à me dire ce qui n'est pas clair.

Merci d'avance

par **kazeriahm** » 01 Déc 2007, 16:29

salut

je suppose donc que tous les paramètres sont réels ?

tu peux étudier la fonction

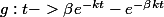
, ses variations puisque le problème est de savoir s'il existe t et t* tels que g(t)=g(t*)

par **ice456** » 01 Déc 2007, 16:37

Oui les paramètres sont réels.

, k

]0 , +

[ ,

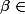
]1, +

[ et