Équation véctorielle

[Triomph]

Bonjour,

Je bloque depuis un petit moment sur une question qui m'est demandée en mathématiques.
La voici:

Déterminez des nombre réels non nuls a, b, c tels que :
a*vect(HA) + b*vect(HB) + c*vect(HC) = 0

(avec vect(HA)=(7;4;-2)
vect(HB)=(2;2;2)
et vect(HC)=(7;5;-1))

Le problème est que je ne sais pas comment résoudre cette équation... J'aimerais que quelqu'un m'explique la démarche.
Si jamais, j'ai d'autres informations sur l'exercice, telles que l'équation cartésienne du plan, un vecteur normal, etc...

Merci à vous.

[hdci]

Bonjour,

Ecrire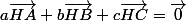

C'est écrire une égalité entre deux vecteurs : le vecteur de droite (vecteur nul) et le vecteur de gauche (somme de trois vecteurs).

Or deux vecteurs sont égaux ssi leurs coordonnées sont égales.

De cette égalité, vous en déduisez trois équations (une pour les abscisses, une pour les ordonnées, une pour les cotes) dont les inconnues sont a, b et c.
Et vous résolvez ce système de trois équations à trois inconnues.

Si vous ne savez pas comment faire pour cette résolution, la méthode immédiate (pas forcément la plus simple, tout dépend du contexte) est d'exprimer dans l'une des équations l'une des inconnues en fonction des deux autres (par exemple, vous écrivez avec les cotes c=fonction de (a,b) et vous reportez cela dans les deux autres équations : cela vous fait maintenant deux équations à deux inconnues que vous avez déjà rencontré en seconde. Quand vous avez trouvé a et b, il n'y a plus qu'à reporter dans c=fonctionde(a,b) pour trouver c.

[mathelot]

bonjour,
l'équation n'a pas de solution car

Les trois vecteur forment une famille libre.

On a donc

remarque: si les coordonnées des trois vecteurs ont été calculées aux questions précédentes d'un énoncé, il y a une erreur de calcul.

[Triomph]

Ah,
D'un côté ça me rassure car je bataille depuis une heure sur l'équation d'un système à 3 inconnues.

Et vect(HC) valait en fait (8;5;-1) et pas (7;5;-1)
La fatigue me joue des tours...

[mathelot]

On a:

[mathelot]

La famille est libre. La famille est
liée.
On peut donc exprimer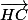 comme combinaison linéaire de 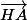et .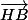

On pose

ce qui donne un système à deux inconnues (x;y) et trois égalités. On procède alors comme dit @hdci

[Triomph]

Merci beaucoup !
Je viens de trouver.