équation complexe avec z^n

[Pisigma]

mais je ne comprends pas d'où tu sors les valeurs qui sont dans ton cos et ton sin

[ijkl]

mais je ne comprends pas d'où tu sors les valeurs qui sont dans ton cos et ton sin

mais écoutez on a le même résultat Pisigma



où est le problème ?

[Pisigma]

je parlais du dans cette expression, pour le cos par exemple

[ijkl]

je parlais du dans cette expression, pour le cos par exemple

bah parce que dans l'expression de z



cos est de période et idem pour sin

on peut prendre tout relatif pour avoir un argument de z

[Black Jack]

commence par rationnaliser ton second membre et cherche le module et un argument du 2d membre

j'ai mis le 2nd membre sous forme a + ib et comme module j'ai trouvé racine de 6 mais je n'arrive pas à trouver l'argument...

Alternative très souvent simplificatrice ...

Rappel :

Si on a Z = z1/z2

|Z| = |z1|/|z2|
arg(Z) = arg(z1) - arg(z2)
*****
z^n = (3 + i*racine de 3)/(1 + i)

z1 = 3 + i.V3 = 2V3.(V3 /2 + i.1/2) --> |z1| = 2V2 et arg(z1) = Pi/6
z2 = 1 + i = V2.(1/V2 + 1/V2 .i) --> |z2| = V2 et arg(z2) = Pi/4

--> |z^n| = |z1|/|z2| = V6
et arg(z^n) = arg(z1) - arg(z2) = Pi/6 - Pi/4 = -Pi/12

z^n = V6 * e^(-Pi/12 + 2k.Pi)

z = 6^(1/(2n)) * e^(-Pi/(12.n) + 2k.Pi/n)

...

[Pisigma]

c'est évidemment comme ça que j'ai procédé mais , d'après ce que j'ai déjà vu, je ne suis pas sûr que c'est la manière utilisée en cours(dommage !)

[ijkl]

...et sinon Pisigma ? tu vois pourquoi dans l'ecriture de ?

on est d'accord que cos et sin sont de période non?



avec et

[Pisigma]

ton ne sert à rien

attention le numérateur de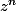 est faux(erreur de recopie sans doute)

[ijkl]

ton ne sert à rien

attention le numérateur de est faux(erreur de recopie sans doute)

oui une erreur de copie

pour le reste certes il ne sert à rien mon mais ta question était pourquoi je l'ai écrit

ça reste vrai (même si il ne sert à rien)

[Pisigma]

Bof!

[ijkl]

Bof!

?

que je sache si on demande un argument de z il vaut mieux l'écrire comme je le fait

car tout argument de z pour tout relatif l sera correct

c'est autre chose si on demande l'argument principal ....

[Pisigma]

le bof se rapporte au

[ijkl]

le bof se rapporte au

oui j'ai compris

d'où ma réponse précédente