simplet a écrit:On peut se servir de la question 2 pour répondre à la question 1:
P divise
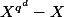
qui n'a pas de racine multiple, étant donné que sa dérivée est constante égale à -1 différent de 0.
Donc P n'a pas de racine double. c'est correct?
Oui mais ce n'est pas logique de raisonner dans ce sens là puisque les questions sont dans l'autre sens...
Ici je pense qu'il vaut mieux remarquer que quand on est dans un corps (resp. anneau commutatif) de caractéristique p, le morphisme de Frobenius
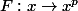
est un morphisme de corps (resp. d'anneaux). Le morphisme
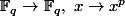
est injectif comme tout morphisme de corps, et comme
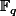
est fini, il est aussi surjectif.
Si
 = Q(X^p) = \sum_{i=0}^n a_i X^{p^i})
, il existe des éléments
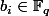
tels que
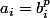
, d'où
 = \( \sum_{i=0}^n b_i X^i \)^p)
, et ça contredit l'irréductibilité de P.
(On vient de montrer que toute extension algébrique d'un corps fini (plus généralement d'un corps pour lequel le morphisme de Frobenius est surjectif) est séparable (le polynôme minimal de tout élément de l'extension est à racines simples), ce que tu verras sûrement si tu fais de la théorie de Galois).
Sinon je n'ai pas tout compris pour ta remarque sur la question 3: Si z est une racine de P alors Fq(z) est isomorphe à Fq[X]/(P) . Donc pour toutes racines z et z' de P on a Fq(z) isomorphe à Fq(z').
Mais ce qu'il faut montrer c'est que Fq(z)=Fq(z') non??
En fait on considère déjà que ce sont les mêmes corps car ils sont isomorphes, c'est pour ça qu'on parle « du » corps de rupture et « du » corps de décomposition d'un polynôme.
Mais ce n'est pas suffisant de savoir que le corps de rupture est unique à isomorphisme près (vrai pour tout polynôme irréductible) pour prouver que corps de rupture = corps de décomposition (pas toujours vrai : par exemple X³ - 2 sur

a un corps de rupture de degré 3 sur

et son corps de décomposition est
)
de degré 6 sur

), ce qu'il faudrait montrer c'est plutôt
 = \mathbb{F}_q(z))
, autrement dit l'extension engendrée par
toutes les racines n'est pas plus grosse que l'extension engendrée par une seule racine, et la question 2 dit justement que si on prend l'extension engendrée par une racine (qui est
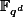
), toutes les racines sont dedans.
