DM de maths (suite et matrice)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 13 Avr 2020, 17:20
par julie0407 » 13 Avr 2020, 17:20
Bonjour tout le monde,
J'ai un DM à rendre pour bientôt mais je suis complètement bloquée... si vous pouvez m'aider ça serait super !
Voici l'énoncé:
Soient U
o et U
1 des nombres réels. On définit la suite (Un))n∈IN par la donnée de Uo et U1 et de la relation de récurrence : U
k+2 = (1 + a)U
k+1 −aUk , k ∈ IN.
1. On pose Uk=
)
Exprimer U
k+1 en fonction de Uk (avec une relation matricielle faisant intervenir la matrice A).
avec A=
)
Ce que j'ai fait actuellement: j'ai développé Uk+1 par rapport à Uk, je trouve donc Uk+1=
)
et je remplace U
k+2 je trouve Uk+1 = A*Uk
2. En déduire Uk en fonction de Uo (avec une relation matricielle faisant intervenir la matrice
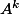
).
j'ai trouvé
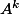
=
+(2^k-1)+1) & 2^k-1 \\ <br /> -2(2^k-1)& 2(2^k-1)+1<br />\end{smallmatrix}\bigr))
Merci de votre aide !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 13 Avr 2020, 17:56
par GaBuZoMeu » 13 Avr 2020, 17:56
Pas clair, ta question. Tu as les réponses pour
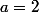
.
Et puis tu notes de la même façon
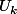
et

. C'est incohérent.
Finalement, dans cet exercice, qu'est-ce que tu as fait et qu'est-ce que tu n'as pas fait ?
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 13 Avr 2020, 18:04
par julie0407 » 13 Avr 2020, 18:04
J'ai recopié mot pour mot mon énoncé et Uk est exprimé par la matrice

...
J'ai fait la question 1 mais je bloque sur la 2.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 13 Avr 2020, 18:11
par GaBuZoMeu » 13 Avr 2020, 18:11
Est-ce que ce n'est pas plutôt

(en distinguant bien minuscules et majuscules).
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 13 Avr 2020, 18:15
par julie0407 » 13 Avr 2020, 18:15
Oui c'est bien ça ^^"

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 13 Avr 2020, 19:49
par Sa Majesté » 13 Avr 2020, 19:49
Dans la 2ème question, on ne te demande pas de calculer explicitement
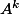
Tu as juste

Après bien sûr, tu peux calculer
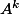
en diagonalisant

Les éléments de la diagonale de ta matrice
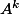
peuvent se simplifier
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 13 Avr 2020, 19:54
par julie0407 » 13 Avr 2020, 19:54
D'accord merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
