Méthode des sécantes

[alibabadu59]

Bonjour
J'aimerais effectuer un algorithme permettant de donner une valeur approchée de la racine carrée de 2 à 10^−100 près à l'aide de la méthode des sécantes,

Pour cela , on construit la suite Un+1=(2+2Un)/(2+Un) et on montre que 0<racine(2)-Un<(1/5)^n
J'ai créé alors cet algorithme mais c'est faux ,on devrait obtenir n=19 et non 144....
Pouvez vous m'indiquer ma(ou mes réponses) s'il vous plaît? merci beaucoup.

Code: Tout sélectionner

a=1
n=0
q=1
while q>10**(-100):
    q=q/5
    n=n+1
    a=(2+2*a)/(2+a)
print (n)

[GaBuZoMeu]

Tu es sûr de chez sûr que ???

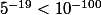
[Black Jack]

(1/5)^n < 10^-100

n > ... (arrondir à l'entier supérieur)

utilise le log décimal.

[alibabadu59]

Mon algorithme n'est pas bon puisque avec la dichotomie j'obtiens une précision à 10^-100 au rang 67, ici 144....
mais je ne vois pas quel algorithme créer...

[GaBuZoMeu]

Tu réponds à côté. D'où sors-tu ce n=19 ??

[alibabadu59]

Oui je sais parce que ça marche pas.
Mon "19" provient d'un programme que j'avais créer il y a quasiment 15 ans sur ma calculatrice voyage 200 au capes pour approximer la racine carrée de 2 par la méthode des sécantes à 10^_100. Je cherche à créer ce programme sur python mais je n'y arrive pas....

[GaBuZoMeu]

Euh ... racine carrée de 2 avec 100 chiffres significatifs sur ta calculette ? Tu galéjes ?

[alibabadu59]

Ça me donnait le rang à partir duquel j'avais cette approximation oui.

[GaBuZoMeu]

Sois plus précis et raconte exactement ce qui te donnait ce 19. Là, tel quel, je ne crois pas un mot de ce que tu écris.

[alibabadu59]

Bon,je sais plus du tout si c'était ma calculatrice qui effectuait ça mais c'est ce que j'avais écrit dans ma leçon que pour n=19 ma suite créée à partir de la méthode des sécantes donnait une approximation de racine carrée de 2 à 10^_100.
C'est certainement possible de le montrer sur python et je cherche comment faire, ou alors j'aimerais juste illustrer le fait que cette méthode est plus performante que la méthode par dichotomie.

[GaBuZoMeu]

Je ne reconnais pas la méthode de la sécante dans la suite que tu as écrite.

Comment obtiens-tu cette suite ?

[alibabadu59]

f(x)=x^2-2 en choisissant a=1 et b=2.
a_n+1= a_n-f(a_n)*(b-a_n)/(f(b)-f(a_n))
et on obtient la suite que j'ai définie plus haut.

[alibabadu59]

Code: Tout sélectionner

def f(x):
    return x**2-2
e=0.01

a=1
while f(a)*f(a+e)>0:
    a=(2+2*a)/(2+a)
print(a)

Sinon cet algorithme me permet de me donner une valeur approchée de racine carrée de 2 à 10^(-2)près. Peut-être qu'il est préférable de travailler sur celui-ci , le transformer pour répondre à ma question, mais je ne vois pas trop comment..