Série de Fourrier - Dimension 1

[Anis1801]

Bonjours à tous et à toutes !

Voila j'ai quelques questions sur les séries de Fourrier C'est pour un projets en Mathématique niveau L3-M1 sur les problèmes aux limites (Neumann/Dirichlet). Surtout n'hésiter pas à me dire si je raconte nimporte quoi c'est vraiment pour que je comprenne mieux le sujet

Enoncé:

On défini la norme hilbertienne sur l'espace de carré intégrable :

.

Avis:

Je suppose que u représente une fonction Intégrable sur l’intervalle tout simplement et que la norme hilbertienne représente une mesure sur l'espace associé. Je pense ne pas avoir vraiment bien compris ce que signifie . Le carré en exposant indique que il s'agit d'un intervalle de dimension 2.Par exemple est un carré en dimension 1 en ?

Enoncé:

On défini ensuite les coéfficients de Fourriers d'une fonction u appartenant à tel que:


Avis:

Bon je pense qu'il n'y a rien d'éxeptionelle à commenter dessus J'ai juste une simple question, le représente 1/(longueur de l'intervalle) ? par Exemple sur , on aurait 1/2?

Question 1:
Si u est , Quelle formule lie et ?

Avis:

Bon alors voilà, je n'ai vraiment pas compris à quoi correspond le . En réalité il y'a juste le pm que je ne comprend pas je n'avais jamais vue ce type d'indice en dessous de C. Si quelqu'un à un avis dessus?

Merci

[LB2]

Bonjour,

cela signifie C1 par morceaux.

La définition de f de classe C1 par morceaux sur [a,b] c'est : il existe un nombre fini de points a1<…<an∈[a,b] tels que f soit de classe C1 sur tout intervalle ]ai,ai+1[ avec i∈{1,…,n−1}.

[Ben314]

Salut,
La définition usuelle (*) de " par morceaux" c'est pas mal plus contraignant que ça vu qu'on demande à ce que la restriction de f à tout intervalle se prolonge sur en une fonction sur cet intervalle.
Bref, il faut qu'en chaque les fonctions et admettent des limites à droite et à gauche.

(*) c.f. Wiki. par exemple.

[LB2]

Effectivement, j'ai recopié un peu vite une définition et c'est important de préciser ce point.

[Anis1801]

Merci pour vos réponse ! Je comprends mieux maintenant le sens de cette indice.

Bon alors je vais être honnête j'ai tenté plusieurs chose pour la question 1 de mon DM mais je ne pense pas être sur la bonne piste.. Je vais rajouter les autres formules indiqué dans mon Sujet pour que vous aillez vous aussi un visuel sur tout le sujet.

On défini la norme hilbertienne sur l'espace de carré intégrable :
.

on défini les coefficients de Fourrier de la forme :

Ces coefficients forment une série de carré sommable satisfaisant la formule de Parseval:



La série de Fourrier associée à u est:

, et .

La série Su s'identifie à u au sens où:



QUESTION 1: Si u est , quelle formule lie Cn(u) et Cn(u')?

QUESTION 2: En déduire que si u est de classe , on a:
, avec C à préciser.

Avis : Bon alors du coups Je me suis dis que pour la question 1 j'allais essayer d'exprimer Cn(u) en fonction de Cn(u') et voir si une formule apparaissait ! J'ai fais une intégration par partie sur la formule de Cn(u) donc j'ai bien réussit mais quand j'ai vue la question 2 (c'est pour ca que je l'ai notée) je me suis dis Que c'étais absolument pas ca qu'il fallait faire ahah.

Donc si quelqu'un à une intuition pour la question 1, sachant que la réponse est sencer être utile dans la question 2. Je veux bien des idées

Merci!!

[LB2]

Pour la question 1, ton idée est bonne, quel résultat obtiens tu?
Pour la question 2, tu peux procéder par récurrence sur k

[Anis1801]

Merci de ta réponse

Alors pour la 1)

J'ai pris: u=u(x) u'=u'(x) v = v'=.

J'ai ensuite fait ma petite intégration par partie classique en utilisant : (uv)'-u'v=uv'.

Ce qui me donne en résultat:

(sauf erreur de signe de ma part mais je ne pense pas en avoir fait )

Une fois que j'en suis arrivé la je me suis dis que je ne voyais pas trop le lien avec la question 2 du DM à part si j'ai rater quelque chose

[LB2]

Le coefficient de Fourier sont des nombres, pas des fonctions. La relation que tu obtiens se simplfiie donc considérablement

[Anis1801]

Bon alors j'ai fais une petite erreur en relisant je m'en suis rendu compte, on obtient:

puisque le fais partie de Cn(u)' et Cn(u').

Je pourrai simplifier en effet tous ca Mais je ne sais pas trop à quoi correspond u(1) et u(-1), et j'ai besoin de ces valeurs pour développer Cn(u)'

Tu as une idée de ceux à quoi peut corréspondre cette valeur?

Ps: J'ai le droit d'insérer le sujet en photo pour que ce soit plus claire? ou c'est interdit par la charte?

Merci

[LB2]

Que signifie pour toi Cn(u)' ?

[Anis1801]

Si je ne dis pas de bétises, Cn(u) c'est la fonction permettant de calculer les coefficients de fourrier grâce à la fonction u.

Cn(u)' est la derrivée de la fonction Cn(u) qui est à pariori une valeur numérique ici, donc logiquement Cn(u)' devrait être égal à 0 puisque c'est la dérivée d'une constante.

C'est ca?

Ce qui laisserai

[LB2]

Cn(u) est effectivement une constante, et tu as donc trouvé la bonne relation.
Voir : https://fr.wikipedia.org/wiki/S%C3%A9ri ... efficients

[Anis1801]

Bonjours à toute et à tous

Merci beaucoups pour m'avoir débloquer sur la question 1 de mon pojet

J'ai pas répondu directement hier pour la question 2 car je cherchais des idées

Alors du coups, vous m'avez conseillé de faire une récurrence sur k.

Donc bon au début je suis dis, on va bidouiller un peu tous ca pour voir quelles sont les différentes formes que je puisse obtenir dans la question 2.

Donc je suis partis de la forume de base à savoir:

.

Je me suis dis tient tient tient:



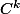
Donc bon, j'ai regardé cette forme et je me suis dis que je devais surement utiliser la question 1 vue que on sait que u est de classe maintenant et que sa nous permettrai de retrouver ce fameux de l'enoncé.

Donc la je sais pas trop quelle piste prendre.. ce que j'ai tenté sa n'a soit rien vraiment donnée. Soit c'étais trop compliqué alors que la solution doit être plus simple..

J'ai tenté d'introduire la formule à l'aide d'une double somme tel que l'on est :

(je me suis peut être trompé sur les indices)

ou alors j'utilise cette forme:



Mais bon je suis pas plus avancé J'ai tenté quelques raisonnements mais je ne vois pas quel est le départ de la réccurence à trouver Si vous avez une idée/intuition je veux bien Thanks LB2

[Anis1801]

Oh okay je dois peut être enfête utiliser la propriété que : ||a+b||<=||a||+||b|| pour obtenir l’inégalité dans un premier temps

[LB2]

Bonjour,

l'idée est de majorer le reste asymptotique de la série de Fourier de u par inégalité triangulaire.
Pour cela, majore chaque terme en norme L2 par une constante fois la valeur absolue de Cn(u) (cette constante dépend de la longueur de l'intervalle).

Or, par récurrence, et la question précédente, on obtient facilement que si u est de classe Ck, alors pour tout n de Z privé de [-N,N], |Cn(u) | est majoré, à une constante multiplicative près, par |Cn(u dérivée k fois)|/n^k, donc par |Cn(u dérivée k fois)|/(N+1)^k

Tu peux ensuite utiliser la formule de Parseval (mais pour u dérivée k fois, pas pour u) pour conclure.

Un lien solide pour faire le point sur les séries de Fourier : http://mpcezanne.fr/Main/Maths/Polycopi ... ourier.pdf

[Anis1801]

Bon alors, je pense avoir à peu près compris la logique..
Je vais écrire ce que je trouve au brouillon mais là c'est vraiment du gros BROUILLON ahah les indices n'ont pas de vraie sens mais c'est juste pour voir si j'ai bien compris le raisonnement que vous vouliez me transmettre !

Bon alors, si je reprend la question 1, on a la forme géneral qui est: (je l'ai retrouver sur le pdf que vous m'avez envoyé).

.

et c'est la ou je pense que ce que je ne sait pas retrouver cette réccurence:


Ensuite on utilise la forme:


On aurait alors, (je sais pas trop comment gerer les indices et je pense que mathématiquement parlant c'est peut-être pas tout à fait ca):

.

En utilsant la formule de Parseval, on a :

.


Alors, là, on a deux options. Soit je raconte nimporte quoi depuis le début Soit c'est à peu près ca mais j'aurai juste pas compris comment trouver la réccurence au début qui mène à cette inégalité:



Dans tout les cas, merci infiniment de ton aide Surtout le lien que tu m'as envoyer il est remplis de formule vachement utile sur les série de fourrier

[Anis1801]

Ah je suis bete..


En toute logique: puisque la série est décroissante elle est donc majoré par qui est le premier terme de la série?

Ahah j'ai bien fait de dormir sa aide à mieux penser

[LB2]

Le premier point est juste, il faudrait le démontrer par une récurrence immédiate.

Ensuite, il faut que tu sois plus précis dans les termes : "la série ... est décroissante" n'a pas de sens.

Que souhaites tu majorer?

[Anis1801]

Bon alors J'ai réussit à faire la réccurence

Au rang 1 c'est vraie d'après la question 1 je l'ai supposé vraie au rang k et demontré au range k+1 en utilisant le même procéder d'intégration par partie mais sur pour faire apparaitre .

Là ou je bloque c'est sur cette partie: "Or, par récurrence, et la question précédente, on obtient facilement que si u est de classe Ck, alors pour tout n de Z privé de [-N,N], |Cn(u) | est majoré, à une constante multiplicative près, par |Cn(u dérivée k fois)|/n^k, donc par |Cn(u dérivée k fois)|/(N+1)^k"

Enfete j'ai du mal à voir comment faire apparaître le N+1 au dénominateur

Ce que je trouve bizzare aussi c'est que dans la formule de Parseval on est: donc que la somme de départ soit sur . Alors que nous on a :


Je me dis que il faudrait sortir le N+1 de cette somme et obtenir quelque chose comme dans la formule de Parseval en .

Enfete il faut juste que j'arrive à trouver de quelle facon je peux faire apparaître ce quotient en N+1 !



Mais c'est pas de votre faute c'est mon cerveau qui bloque x)