Pour passer de a) à c) on considère le temps d'arrêt borné
Martingale de l'excédent
Re: martingale de l'excédent
Je suis d'accord avec cela. Mais dans les cours que je suis retourné voir on n'a généralement pas les hypothèses b) et c).
Pour passer de a) à c) on considère le temps d'arrêt borné) , puis on passe à la limite en T.
, puis on passe à la limite en T.
Pour passer de a) à c) on considère le temps d'arrêt borné
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: martingale de l'excédent
J'ai testé une martingale différente :
Charles a n jetons (n entre 1 et 24) ; il joue jusqu'à ce qu'il arrive à 25 jetons (ou jusqu'à ce qu'il n'ait plus le moindre jeton).
Jusque là, rien de nouveau.
Mais si Charles tire 3 coups gagnants consécutifs, alors il décide de quitter la partie.
On peut imaginer que cette stratégie est gagnante. Souvent, la séquence va se terminer par 3 victoires consécutives, C'est donc a priori favorable pour Charles.
J'ai bâti la matrice de Markov de cette martingale (et je suis fier de ça, donc je le dis). J'ai élevé cette matrice à la puissance 256, et j'ai calculé l'espérance pour chacune des valeurs de n. Et surprise, la stratégie n'est absolument pas gagnante. Equilibre parfait.
J'avais commencé cette réflexion avant que Sylviel ne parle du théorème de Doob.
Et la question que je pose, c'est : est-on toujours dans le cadre du théorème de Doob ?
Je pense que la réponse est oui, mais je n'en suis pas sûr à 100%.
Charles a n jetons (n entre 1 et 24) ; il joue jusqu'à ce qu'il arrive à 25 jetons (ou jusqu'à ce qu'il n'ait plus le moindre jeton).
Jusque là, rien de nouveau.
Mais si Charles tire 3 coups gagnants consécutifs, alors il décide de quitter la partie.
On peut imaginer que cette stratégie est gagnante. Souvent, la séquence va se terminer par 3 victoires consécutives, C'est donc a priori favorable pour Charles.
J'ai bâti la matrice de Markov de cette martingale (et je suis fier de ça, donc je le dis). J'ai élevé cette matrice à la puissance 256, et j'ai calculé l'espérance pour chacune des valeurs de n. Et surprise, la stratégie n'est absolument pas gagnante. Equilibre parfait.
J'avais commencé cette réflexion avant que Sylviel ne parle du théorème de Doob.
Et la question que je pose, c'est : est-on toujours dans le cadre du théorème de Doob ?
Je pense que la réponse est oui, mais je n'en suis pas sûr à 100%.
Re: martingale de l'excédent
La martingale (au sens technique des probas) est la même, ce qui change c'est le temps d'arrêt - mais c'est toujours un temps d'arrêt. Et la condition c) de l'énoncé du théorème de Doob (version wikipedia anglais) est bien sûr toujours vérifiée. Donc, même conclusion : espérance de gain nulle de chez nul.
lycéen95 : quelle est la taille de ta matrice de transition ? 89, je dirais , et je ne vois pas comment tu pourrais faire moins. Si ?
lycéen95 : quelle est la taille de ta matrice de transition ? 89, je dirais , et je ne vois pas comment tu pourrais faire moins. Si ?
Re: martingale de l'excédent
J'ai fait une matrice 104x104.
Aucune optimisation, voire pas mal de gâchis assumé. Si je compte bien, je pouvais réduire à 92x92.
Aucune optimisation, voire pas mal de gâchis assumé. Si je compte bien, je pouvais réduire à 92x92.
Re: martingale de l'excédent
J'ai 89. Qui dit moins ? 
0 et 25
4 à 24 en PPP (23 états absorbants) (P=pile, gagnant)
3 à 23 en PP pas PPP
2 à 22 en P pas PP
1 à 24 en le reste

0 et 25
4 à 24 en PPP (23 états absorbants) (P=pile, gagnant)
3 à 23 en PP pas PPP
2 à 22 en P pas PP
1 à 24 en le reste
Re: martingale de l'excédent
Je ne vois pas pourquoi tu exclues les cas :
24PP
24P
23P
On a (au maximum) 26 valeurs et 4 états possibles pour chaque valeur. D'où le 104 de mon tableau.
Les 26 valeurs: 0 à 25 ;
Les 4 états possibles : F, P, PP, ou PPP : PP signifie que les 2 derniers tirages ont été P ; F signifie que le dernier tirage a été F.
Certains états sont impossibles : 0P 0PP ou 0PPP sont impossibles, on ne peut pas être à 0 si le dernier tirage était un gain.
Idem 25F est impossible , pour la même raison.
24F est impossible aussi : on ne peut pas être à 24 si on vient de perdre le dernier tirage.
Et 1P , 1PP , 1PPP , 2PP, 3PPP sont impossibles : si j'ai 3 jetons, et que les 3 derniers tirages sont positifs, c'est que j'ai déjà été à découvert.
Et certains états sont possibles, mais c'est inutile de les distinguer : 25P 25PP et 25PPP : J'utilise 3 valeurs différentes, alors qu'une seule suffirait.
On a donc 10 cas qui sont impossibles (0P, 0PP, 0PPP, 1P, 1PP, 1PPP, 2PP, 2PPP, 3PP 24F), et 2 cas qui sont redondants : 104-10-2=92.
Le cas 24F est impossible, mais il faut quand même le garder. L'idée est de tester : Charles commence avec n jetons, et on étudie la martingale. Dans le cas n=24 (et uniquement dans ce cas), on a besoin du cas 24F. Il y a des points qui sont absorbants ; disons que 24F est 'anti-absorbant', ou répulsif.
Donc 93 plutôt que 92.
24PP
24P
23P
On a (au maximum) 26 valeurs et 4 états possibles pour chaque valeur. D'où le 104 de mon tableau.
Les 26 valeurs: 0 à 25 ;
Les 4 états possibles : F, P, PP, ou PPP : PP signifie que les 2 derniers tirages ont été P ; F signifie que le dernier tirage a été F.
Certains états sont impossibles : 0P 0PP ou 0PPP sont impossibles, on ne peut pas être à 0 si le dernier tirage était un gain.
Idem 25F est impossible , pour la même raison.
24F est impossible aussi : on ne peut pas être à 24 si on vient de perdre le dernier tirage.
Et 1P , 1PP , 1PPP , 2PP, 3PPP sont impossibles : si j'ai 3 jetons, et que les 3 derniers tirages sont positifs, c'est que j'ai déjà été à découvert.
Et certains états sont possibles, mais c'est inutile de les distinguer : 25P 25PP et 25PPP : J'utilise 3 valeurs différentes, alors qu'une seule suffirait.
On a donc 10 cas qui sont impossibles (0P, 0PP, 0PPP, 1P, 1PP, 1PPP, 2PP, 2PPP, 3PP 24F), et 2 cas qui sont redondants : 104-10-2=92.
Le cas 24F est impossible, mais il faut quand même le garder. L'idée est de tester : Charles commence avec n jetons, et on étudie la martingale. Dans le cas n=24 (et uniquement dans ce cas), on a besoin du cas 24F. Il y a des points qui sont absorbants ; disons que 24F est 'anti-absorbant', ou répulsif.
Donc 93 plutôt que 92.
Re: martingale de l'excédent
Je ne vois pas pourquoi tu exclues les cas : 24PP, 24P, 23P
Je ne les exclus pas, je les regroupe avec d'autres.
Pour 25 qui est absorbant, pas besoin de faire de distinction.
Pour 24, la seule distinction utile est entre PPP (état absorbant) et le reste.
Pour 23, la seule distinction à faire est entre PPP (état absorbant), PP et le reste.
À noter à chaque fois que "le reste" inclut les cas où Charles débute avec ce nombre de jetons.
Le 24 reste peut évoluer en 25 ou en 23 reste (ni PPP ni PP).
Le 23 reste peut évoluer en 24 reste (pas PPP) ou en 22 reste.
Je maintiens le 89. Tu es d'accord maintenant, lycéen95, ou il y a encore un problème ?
Re: martingale de l'excédent
Bien vu. Si on est arrivé à 24 après P ou après PP, peu importe de faire la distinction. Don on peut économiser une configuration.
Et si on arrive à 23 après P ou après F, peu importe de faire la distinction , On économise une 2ème configuration.
Pas trop le temps de recompter, mais j'ai l'impression que ça me fait toujours 90.
Et si on arrive à 23 après P ou après F, peu importe de faire la distinction , On économise une 2ème configuration.
Pas trop le temps de recompter, mais j'ai l'impression que ça me fait toujours 90.
Re: martingale de l'excédent
GaBuZoMeu a écrit:La martingale (au sens technique des probas) est la même, ce qui change c'est le temps d'arrêt - mais c'est toujours un temps d'arrêt. Et la condition c) de l'énoncé du théorème de Doob (version wikipedia anglais) est bien sûr toujours vérifiée. Donc, même conclusion : espérance de gain nulle de chez nul.
Parfaitement d'accord. L'espérance de gain reste nul. En revanche on ne peut plus conclure directement sur les probas d'atteindre 25 / 0 à partir de cela puisqu'il y a maintenant d'autres fin possible.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: martingale de l'excédent
Lyceen95 a écrit une matrice de transition. Il lui suffit de calculer son projecteur spectral associé à la valeur propre 1 pour avoir la réponse à cette question. 

Re: martingale de l'excédent
Effectivement, tu avoueras que c'est moins direct ^^
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: martingale de l'excédent
Moins direct que quoi ? Comme tu l'as fait remarquer, le théorème de Doob ne permet pas de répondre à la question "Si Charles commence avec 20 jetons, avec quelle probabilité ressortira-t-il avec n jetons ?". Le calcul du projecteur spectral répond, lui, à cette question. Connais-tu un moyen plus direct d'y répondre ?
Re: martingale de l'excédent

Voici l'énoncé que j'ai évoqué.
Il utilise les probabilités conditionnelles et la notion de fonction génératrice d'une variable aléatoire discrète, mais ne nécessite pas la connaissance des chaines de Markov.
Les règles du jeu entre le joueur et la banque sont légèrement différentes, mais il me semble que l'on peut adapter l'énoncé, et sa résolution.
Re: martingale de l'excédent
Hum, c'est du genre processus de Galton-Watson ?
Ça ne paraît pas vraiment du genre de l'histoire racontée dans l'exercice, puisque dans cet exercice Charles ne mise qu'un jeton à la fois. Si tu as une idée d'adaptation, peux-tu la préciser s'il te plaît ?
Ça ne paraît pas vraiment du genre de l'histoire racontée dans l'exercice, puisque dans cet exercice Charles ne mise qu'un jeton à la fois. Si tu as une idée d'adaptation, peux-tu la préciser s'il te plaît ?
Re: martingale de l'excédent
Effectivement, j'étais beaucoup trop optimiste! Dans l'exercice que j'ai exposé, on a une relation de récurrence simple entre les fonctions génératrices, de type Galton Watson, qui permet d'en déduire tout le reste.
Dans ton exercice, on peut essayer de trouver une relation de récurrence entre les fonctions génératrices, mais il y a des effets de bord, je n'ai pas réussi à faire aboutir le même raisonnement.
En revanche, voici un raisonnement élémentaire, qui peut-être a déjà été donné, mais je le trouve assez élégant (il n'est pas de moi mais de http://culturemath.ens.fr/maths/pdf/proba/marchesZ.pdf)
Les règles : Le joueur dispose d'un capital initial (ici
(ici 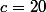 ) et d'un objectif à atteindre
) et d'un objectif à atteindre  (ici
(ici 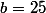 ). La pièce est équilibrée. Si le joueur arrive à 0 ou à b, le jeu s'arrête.
). La pièce est équilibrée. Si le joueur arrive à 0 ou à b, le jeu s'arrête.
Rigoureusement, on doit justifier que le jeu s'arrête presque sûrement.
Notons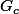 l'évènement : "le joueur atteint son objectif, avec un capital initial de c" et
l'évènement : "le joueur atteint son objectif, avec un capital initial de c" et 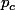 sa probabilité.
sa probabilité.
On peut montrer la propriété d'harmonicité :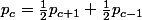
pour tout compris strictement entre
compris strictement entre  et
et  .
.
Pour cela, on utilise les probabilités totales, en conditionnant par le résultat du premier lancer. Li'dée étant que si le premier lancer est favorable au joueur, c'est "comme si" le jeu recommençait de zéro, mais avec un capital augmenté d'une unité.
La suite ( ) vérifie donc une récurrence linéaire d'ordre 2 :
) vérifie donc une récurrence linéaire d'ordre 2 : 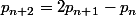
L'équation caractéristique admet une racine double r=1.
La solution générale est donc donnée par la formule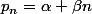
Or, on connait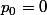 et
et 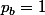
d'où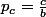 . L'application numérique donne bien une proba de gain de 20/25 = 80%.
. L'application numérique donne bien une proba de gain de 20/25 = 80%.
Remarque : L'idée intéressante est de pouvoir faire varier le capital initial, ce qui permet de calculer simplement la probabilité cherchée sans avoir à dénombrer des chemins.
Bonus : on peut adapter cette méthode à des jeux non équilibrés comme la roulette (avec probabilité de gain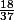 ) et on a une jolie formule en fonction de
) et on a une jolie formule en fonction de  et
et  .
.
Dans ton exercice, on peut essayer de trouver une relation de récurrence entre les fonctions génératrices, mais il y a des effets de bord, je n'ai pas réussi à faire aboutir le même raisonnement.
En revanche, voici un raisonnement élémentaire, qui peut-être a déjà été donné, mais je le trouve assez élégant (il n'est pas de moi mais de http://culturemath.ens.fr/maths/pdf/proba/marchesZ.pdf)
Les règles : Le joueur dispose d'un capital initial
Rigoureusement, on doit justifier que le jeu s'arrête presque sûrement.
Notons
On peut montrer la propriété d'harmonicité :
pour tout
Pour cela, on utilise les probabilités totales, en conditionnant par le résultat du premier lancer. Li'dée étant que si le premier lancer est favorable au joueur, c'est "comme si" le jeu recommençait de zéro, mais avec un capital augmenté d'une unité.
La suite (
L'équation caractéristique admet une racine double r=1.
La solution générale est donc donnée par la formule
Or, on connait
d'où
Remarque : L'idée intéressante est de pouvoir faire varier le capital initial, ce qui permet de calculer simplement la probabilité cherchée sans avoir à dénombrer des chemins.
Bonus : on peut adapter cette méthode à des jeux non équilibrés comme la roulette (avec probabilité de gain
Modifié en dernier par LB2 le 11 Jan 2020, 02:52, modifié 1 fois.
Re: martingale de l'excédent
PS. En fait cette belle idée revient à la recherche du fameux projecteur spectral (coucou le revoici !). La matrice de transition peut se mettre par blocs sous la forme
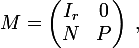
où le bloc identité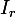 correspond aux
correspond aux  états absorbants. Le projecteur spectral associé à la valeur propre 1 est alors de la forme
états absorbants. Le projecteur spectral associé à la valeur propre 1 est alors de la forme
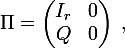
L'histoire d'écrire la formule des probabilités totales en conditionnant au premier lancer revient très exactement à écrire la formule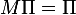 , qui elle-même revient à
, qui elle-même revient à 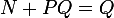 ; si on regarde, cette équation matricielle correspond exactement aux relations de récurrence et aux conditions au bord du message de LB2. Puisque
; si on regarde, cette équation matricielle correspond exactement aux relations de récurrence et aux conditions au bord du message de LB2. Puisque 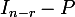 est inversible (le rayon spectral de
est inversible (le rayon spectral de 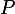 est
est 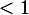 ),
), 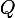 s'obtient comme
s'obtient comme ^{-1} N) .
.
Cette méthode s'applique aussi directement à la version modifiée par Lycéen95 de l'exercice, où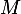 est de taille
est de taille 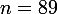 et
et 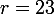 .
.
où le bloc identité
L'histoire d'écrire la formule des probabilités totales en conditionnant au premier lancer revient très exactement à écrire la formule
Cette méthode s'applique aussi directement à la version modifiée par Lycéen95 de l'exercice, où
Re: martingale de l'excédent
Bon, puisque Lycéen95 ne se décide pas à calculer son projecteur spectral, je m'y colle. Le plus long est d'entrer la matrice de transition M. Je prends les états dans l'ordre :
0 jeton
k jetons avec en dernier 3P, pour k de 4 à 24
25 jetons
k jetons avec 2P, pour k de 3 à 23
k jetons avec 1P, pour k de 2 à 22
k jetons avec 0P, pour k de 1 à 22
23 jetons avec <2P
24 jetons avec <3P
Le code SageMath, avec les mêmes notations N,P,Q que ci-dessus :
et maintenant on peut demander :
avec comme réponse :
En démarrant avec 20 jetons, probabilité de sortir avec
0 jeton : 16384/3577029 soit 0.458 %
4 jetons : 4096/3577029 soit 0.115 %
5 jetons : 2048/1192343 soit 0.172 %
6 jetons : 8192/3577029 soit 0.229 %
7 jetons : 3584/1192343 soit 0.301 %
8 jetons : 14080/3577029 soit 0.394 %
9 jetons : 6144/1192343 soit 0.515 %
10 jetons : 24128/3577029 soit 0.675 %
11 jetons : 224/25369 soit 0.883 %
12 jetons : 41344/3577029 soit 1.16 %
13 jetons : 18040/1192343 soit 1.51 %
14 jetons : 70844/3577029 soit 1.98 %
15 jetons : 1344/51841 soit 2.59 %
16 jetons : 121393/3577029 soit 3.39 %
17 jetons : 105937/2384686 soit 4.44 %
18 jetons : 208010/3577029 soit 5.81 %
19 jetons : 15449/202952 soit 7.61 %
20 jetons : 5702887/57232464 soit 9.96 %
21 jetons : 311049/2384686 soit 13.0 %
22 jetons : 39088169/228929856 soit 17.1 %
23 jetons : 34111385/152619904 soit 22.4 %
24 jetons : 4873055/114464928 soit 4.26 %
25 jetons : 4873055/457859712 soit 1.06 %
Espérance du nombre de jetons de sortie :
20 jetons
L'espérance de gain, c.-à-d. l'espérance du nombre de jetons de sortie moins le nombre de jetons de départ, est bien sûr nulle, le théorème de l'arrêt de Doob nous l'avait déjà dit. Mais le théorème de Doob ne nous disait rien sur les probabilités des différents cas de sortie pour cet exercice modifié Lycéen95.
Concrètement, qu'entraîne le fait que l'espérance de gain est nulle ? Ça entraîne que, si Charles revient jouer chaque soir avec la même stratégie, la moyenne de ses gains tendra presque sûrement vers 0. La loi des grands nombres est dure, mais c'est la loi ! Aucun espoir de s'assurer un revenu de cette façon.
0 jeton
k jetons avec en dernier 3P, pour k de 4 à 24
25 jetons
k jetons avec 2P, pour k de 3 à 23
k jetons avec 1P, pour k de 2 à 22
k jetons avec 0P, pour k de 1 à 22
23 jetons avec <2P
24 jetons avec <3P
Le code SageMath, avec les mêmes notations N,P,Q que ci-dessus :
- Code: Tout sélectionner
M=matrix(QQ,89,89)
for i in range(23) :
M[i,i]=1
for i in range(23,44):
M[i,i-22]=1/2; M[i,i+43]=1/2
for i in range(44,65) :
M[i,i-21]=1/2; M[i,i+21]=1/2
M[65,44]=1/2; M[65,0]=1/2
for i in range(66,86) :
M[i,i-21]=1/2; M[i,i-1]=1/2
M[86,87]=1/2; M[86,85]=1/2
M[87,88]=1/2; M[87,86]=1/2
M[88,22]=1/2; M[88,87]=1/2
N=M.submatrix(23,0,66,23)
P=M.submatrix(23,23,66,66)
Q=(identity_matrix(QQ,66)-P)^(-1)*N
et maintenant on peut demander :
- Code: Tout sélectionner
k=20
V=Q.row(41+k)
print 'En démarrant avec',k,'jetons, probabilité de sortir avec'
print '0 jeton :',V[0],'soit',(100*V[0]).n(12),'%'
for i in range(1,23) :
print i+3,'jetons :',V[i],'soit',(100*V[i]).n(12),'%'
print 'Espérance du nombre de jetons de sortie :'
print sum((i+3)*V[i] for i in range(1,23)), 'jetons'
avec comme réponse :
En démarrant avec 20 jetons, probabilité de sortir avec
0 jeton : 16384/3577029 soit 0.458 %
4 jetons : 4096/3577029 soit 0.115 %
5 jetons : 2048/1192343 soit 0.172 %
6 jetons : 8192/3577029 soit 0.229 %
7 jetons : 3584/1192343 soit 0.301 %
8 jetons : 14080/3577029 soit 0.394 %
9 jetons : 6144/1192343 soit 0.515 %
10 jetons : 24128/3577029 soit 0.675 %
11 jetons : 224/25369 soit 0.883 %
12 jetons : 41344/3577029 soit 1.16 %
13 jetons : 18040/1192343 soit 1.51 %
14 jetons : 70844/3577029 soit 1.98 %
15 jetons : 1344/51841 soit 2.59 %
16 jetons : 121393/3577029 soit 3.39 %
17 jetons : 105937/2384686 soit 4.44 %
18 jetons : 208010/3577029 soit 5.81 %
19 jetons : 15449/202952 soit 7.61 %
20 jetons : 5702887/57232464 soit 9.96 %
21 jetons : 311049/2384686 soit 13.0 %
22 jetons : 39088169/228929856 soit 17.1 %
23 jetons : 34111385/152619904 soit 22.4 %
24 jetons : 4873055/114464928 soit 4.26 %
25 jetons : 4873055/457859712 soit 1.06 %
Espérance du nombre de jetons de sortie :
20 jetons
L'espérance de gain, c.-à-d. l'espérance du nombre de jetons de sortie moins le nombre de jetons de départ, est bien sûr nulle, le théorème de l'arrêt de Doob nous l'avait déjà dit. Mais le théorème de Doob ne nous disait rien sur les probabilités des différents cas de sortie pour cet exercice modifié Lycéen95.
Concrètement, qu'entraîne le fait que l'espérance de gain est nulle ? Ça entraîne que, si Charles revient jouer chaque soir avec la même stratégie, la moyenne de ses gains tendra presque sûrement vers 0. La loi des grands nombres est dure, mais c'est la loi ! Aucun espoir de s'assurer un revenu de cette façon.

Re: martingale de l'excédent
Je n'ai pas calculé le projecteur spectral, pour différentes raisons.
La première, c'est que je ne sais pas faire. C'est une très bonne raison. On pourrait me rétorquer : c'est simple, essaie de comprendre ... ce à quoi je vais répondre que certes, c'est simple, mais il y a des tas de choses simples que je ne fais pas, parce qu'elles ne m'amusent pas.
La deuxième raison, c'est que un calcul partiel (256 étapes en l'occurrence), c'est une très bonne approximation. C'est même peut être mieux qu'un calcul complet, parce que dans la vraie vie, le 'croupier' qui lance la pièce ne va pas la lancer des millions de fois, il va s'arrêter à un moment ou un autre. J'avais hésité dans ma formulation du problème , à ajouter une clause : quoi qu'il arrive Charles arrêtera de jouer après 256 parties maximum.
PS : quelle idée d'avoir appelé notre joueur Charles. Je cite :
Charles attend ... Et pourquoi pas Charlatan tant que tu y es, petit coquin !
La première, c'est que je ne sais pas faire. C'est une très bonne raison. On pourrait me rétorquer : c'est simple, essaie de comprendre ... ce à quoi je vais répondre que certes, c'est simple, mais il y a des tas de choses simples que je ne fais pas, parce qu'elles ne m'amusent pas.
La deuxième raison, c'est que un calcul partiel (256 étapes en l'occurrence), c'est une très bonne approximation. C'est même peut être mieux qu'un calcul complet, parce que dans la vraie vie, le 'croupier' qui lance la pièce ne va pas la lancer des millions de fois, il va s'arrêter à un moment ou un autre. J'avais hésité dans ma formulation du problème , à ajouter une clause : quoi qu'il arrive Charles arrêtera de jouer après 256 parties maximum.
PS : quelle idée d'avoir appelé notre joueur Charles. Je cite :
Charles attend, il observe un certain nombre de tirages et note les résultats jusqu'à ce qu'il constate que face est en avance de 5.
Charles attend ... Et pourquoi pas Charlatan tant que tu y es, petit coquin !
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
